Lafforgue and Genestier-Lafforgue have constructed the global and (semisimplified) local Langlands correspondences for arbitrary reductive groups over function fields. We establish various properties of these correspondences regarding functoriality for cyclic base change: For 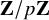 $\mathbf {Z}/p\mathbf {Z}$-extensions of global function fields, we prove the existence of base change for mod p automorphic forms on arbitrary reductive groups. For
$\mathbf {Z}/p\mathbf {Z}$-extensions of global function fields, we prove the existence of base change for mod p automorphic forms on arbitrary reductive groups. For 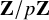 $\mathbf {Z}/p\mathbf {Z}$-extensions of local function fields, we construct a base change homomorphism for the mod p Bernstein center of any reductive group. We then use this to prove existence of local base change for mod p irreducible representation along
$\mathbf {Z}/p\mathbf {Z}$-extensions of local function fields, we construct a base change homomorphism for the mod p Bernstein center of any reductive group. We then use this to prove existence of local base change for mod p irreducible representation along 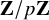 $\mathbf {Z}/p\mathbf {Z}$-extensions, and that Tate cohomology realizes base change descent, verifying a function field version of a conjecture of Treumann-Venkatesh.
$\mathbf {Z}/p\mathbf {Z}$-extensions, and that Tate cohomology realizes base change descent, verifying a function field version of a conjecture of Treumann-Venkatesh.
The proofs are based on equivariant localization arguments for the moduli spaces of shtukas. They also draw upon new tools from modular representation theory, including parity sheaves and Smith-Treumann theory. In particular, we use these to establish a categorification of the base change homomorphism for mod p spherical Hecke algebras, in a joint appendix with Gus Lonergan.
 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
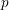 $p$
-adic Langlands program for
$p$
-adic Langlands program for
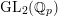 $\operatorname{GL}_{2}(\mathbb{Q}_{p})$
$\operatorname{GL}_{2}(\mathbb{Q}_{p})$
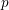 $p$ local-global compatibility for
$p$ local-global compatibility for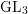 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
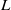 -packets
-packets