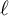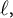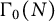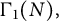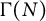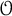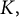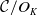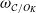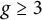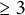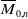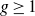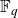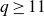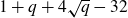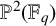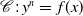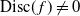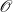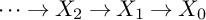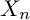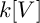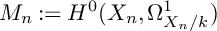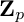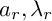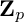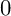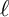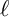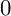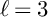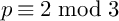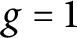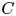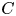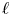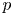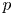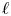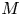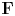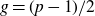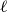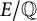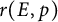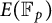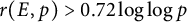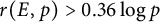Refine search
Actions for selected content:
60 results
The p-adic limits of class numbers in
 ${\mathbb{Z}}_p$-towers
${\mathbb{Z}}_p$-towers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 23 May 2025, pp. 299-329
- Print publication:
- September 2025
-
- Article
- Export citation
Ordinary isogeny graphs with level structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 27 March 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric local systems on the projective line minus four points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 01 July 2025, pp. 536-554
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chai's conjecture for semiabelian Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 120-147
- Print publication:
- January 2025
-
- Article
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refinements of Katz–Sarnak theory for the number of points on curves over finite fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 January 2024, pp. 400-425
- Print publication:
- April 2025
-
- Article
- Export citation
Tropical invariants for binary quintics and reduction types of Picard curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 65-87
- Print publication:
- January 2024
-
- Article
- Export citation
Lower bounds on the maximal number of rational points on curves over finite fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 213-238
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
- Export citation
Galois representations of superelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 356-382
- Print publication:
- May 2023
-
- Article
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOUNDARY OF THE p-RANK
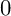 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 687-712
- Print publication:
- June 2023
-
- Article
- Export citation
The monodromy of unit-root F-isocrystals with geometric origin
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 334-365
- Print publication:
- February 2022
-
- Article
- Export citation
Wild Galois representations: a family of hyperelliptic curves with large inertia image
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 619-633
- Print publication:
- November 2022
-
- Article
- Export citation
An elliptic curve analogue of Pillai’s lower bound on primitive roots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 496-505
- Print publication:
- June 2022
-
- Article
- Export citation
Corrigendum: Around
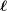 $\boldsymbol{\ell }$-independence
$\boldsymbol{\ell }$-independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1262-1274
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation