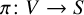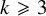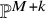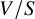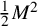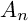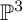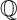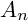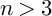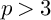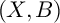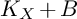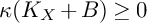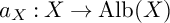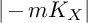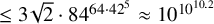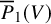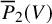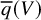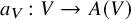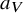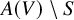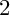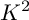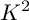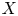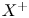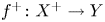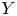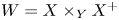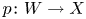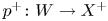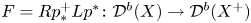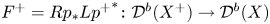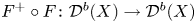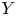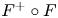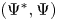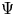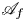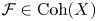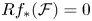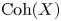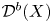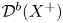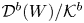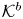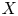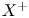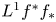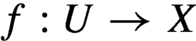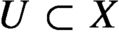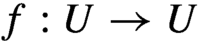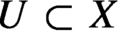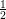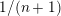41 results
Birationally rigid Fano-Mori fibre spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
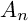 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 970-1021
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
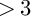 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
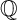 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Nonsolidity of uniruled varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 August 2023, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remark on complements on surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic dynamics of the pentagram map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 3460-3505
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher index Fano varieties with finitely many birational automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 02 December 2022, pp. 2033-2045
- Print publication:
- November 2022
-
- Article
- Export citation
Intersection theory of nef b-divisor classes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1563-1594
- Print publication:
- July 2022
-
- Article
- Export citation
BIRATIONAL RIGIDITY OF ORBIFOLD DEGREE 2 DEL PEZZO FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 02 June 2022, pp. 888-921
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flops and spherical functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 01 August 2022, pp. 1125-1187
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE EMBEDDINGS OF THE HEISENBERG GROUP INTO THE CREMONA GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 09 March 2021, pp. 243-251
- Print publication:
- January 2022
-
- Article
- Export citation
Strong submeasures and applications to non-compact dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 December 2020, pp. 287-309
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation
FANO HYPERSURFACES WITH ARBITRARILY LARGE DEGREES OF IRRATIONALITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 08 May 2020, e24
-
- Article
-
- You have access
- Open access
- Export citation
Two polarised K3 surfaces associated to the same cubic fourfold
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 51-64
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
Projective Reconstruction in Algebraic Vision
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 13 November 2019, pp. 592-609
- Print publication:
- September 2020
-
- Article
- Export citation
K-stability of birationally superrigid Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1845-1852
- Print publication:
- September 2019
-
- Article
- Export citation