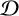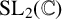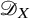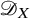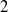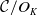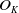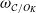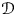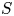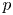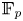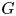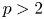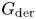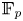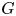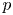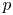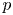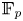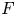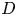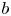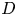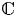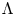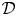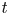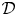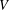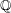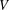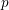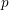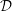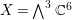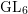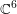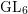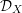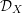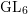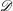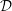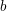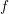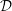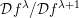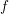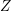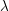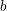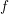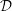35 results
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Hyperplane Arrangements Satisfy (Un)Twisted Logarithmic Comparison Theorems, Applications to
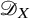 $\mathscr {D}_{X}$-modules
$\mathscr {D}_{X}$-modules
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drinfeld's lemma for F-isocrystals, II: Tannakian approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 90-119
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Weighted Hodge ideals of reduced divisors
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 June 2023, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative regular Riemann–Hilbert correspondence II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1413-1465
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A BERNSTEIN–SATO POLYNOMIAL OF A MEROMORPHIC FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 715-733
- Print publication:
- September 2023
-
- Article
- Export citation
Hodge filtration on local cohomology, Du Bois complex and local cohomological dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 03 October 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hecke action on the principal block
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 19 July 2022, pp. 953-1019
- Print publication:
- May 2022
-
- Article
- Export citation
Central elements in affine mod p Hecke algebras via perverse
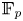 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
A generalization of the b-function lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 07 September 2021, pp. 2199-2214
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irregular perverse sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 573-624
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Log
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e3
-
- Article
-
- You have access
- Open access
- Export citation
Summands of theta divisors on Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 08 July 2020, pp. 1457-1475
- Print publication:
- July 2020
-
- Article
- Export citation
HODGE IDEALS FOR
 $\mathbb{Q}$-DIVISORS,
$\mathbb{Q}$-DIVISORS, 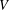 $V$-FILTRATION, AND MINIMAL EXPONENT
$V$-FILTRATION, AND MINIMAL EXPONENT
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 17 April 2020, e19
-
- Article
-
- You have access
- Open access
- Export citation
BERNSTEIN–SATO ROOTS FOR MONOMIAL IDEALS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 20 March 2020, pp. 25-34
- Print publication:
- December 2021
-
- Article
- Export citation
EQUIVARIANT
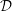 ${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 29 November 2019, pp. 61-82
- Print publication:
- September 2021
-
- Article
- Export citation
AROUND THE NEARBY CYCLE FUNCTOR FOR ARITHMETIC
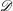 $\mathscr{D}$-MODULES
$\mathscr{D}$-MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 28 August 2019, pp. 1-28
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
IRREGULAR HODGE FILTRATION OF SOME CONFLUENT HYPERGEOMETRIC SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 May 2019, pp. 627-668
- Print publication:
- March 2021
-
- Article
- Export citation
On
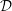 ${\mathcal{D}}$-modules related to the
${\mathcal{D}}$-modules related to the 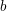 $b$-function and Hamiltonian flow
$b$-function and Hamiltonian flow
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 12 October 2018, pp. 2426-2440
- Print publication:
- November 2018
-
- Article
- Export citation