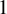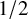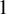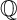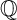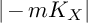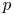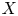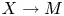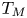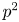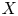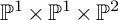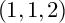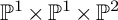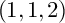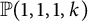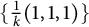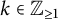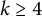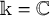70 results
NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-24
-
- Article
- Export citation
Nef vector bundles on a quadric threefold with first Chern class two
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 January 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 ${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
${\mathbb {Q}}$-FANO THREEFOLDS AND LAURENT INVERSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-47
-
- Article
- Export citation
FANO FOURFOLDS WITH LARGE ANTICANONICAL BASE LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIGNESS OF THE TANGENT BUNDLE OF A FANO THREEFOLD WITH PICARD NUMBER TWO
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
Torsion points and concurrent exceptional curves on del Pezzo surfaces of degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symmetric tensors on the intersection of two quadrics and Lagrangian fibration
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds on the height of K-semistable Fano varieties I, the toric case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 10 October 2024, pp. 2366-2406
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL GEOMETRY OF SEXTIC DOUBLE SOLIDS WITH A COMPOUND
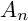 $A_n$ SINGULARITY
$A_n$ SINGULARITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 970-1021
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stable smooth Fano threefolds of Picard rank two
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 March 2024, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE UPPER BOUND FOR ANTI-CANONICAL VOLUMES OF SINGULAR FANO THREEFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 2631-2646
- Print publication:
- November 2024
-
- Article
-
- You have access
- HTML
- Export citation
K-stability of birationally superrigid Fano 3-fold weighted hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 October 2023, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ANTI-CANONICAL GEOMETRY OF WEAK
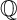 $\mathbb {Q}$-FANO THREEFOLDS, III
$\mathbb {Q}$-FANO THREEFOLDS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 23-47
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Nonsolidity of uniruled varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 August 2023, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Projective varieties with nef tangent bundle in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1974-1999
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-STABLE DIVISORS IN
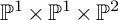 $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE
$\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^2$ OF DEGREE 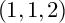 $(1,1,2)$
$(1,1,2)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 686-714
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the smooth blowups of
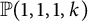 $\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties
$\mathbb {P}(1,1,1,k)$ in torus-invariant subvarieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 March 2023, pp. 1152-1163
- Print publication:
- December 2023
-
- Article
- Export citation
The existence of the Kähler–Ricci soliton degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 March 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
























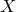
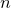
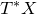
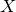
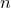
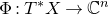
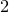
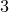
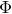
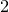
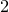
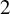
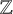
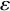
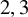
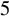
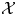
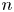
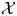
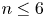
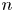
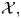
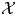
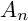
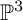
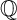
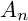
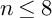
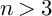
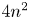
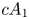
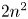
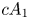
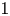
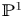
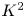
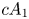
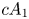
 and
and  are K-stable, and we also prove that smooth Fano threefolds in the family
are K-stable, and we also prove that smooth Fano threefolds in the family 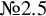 that satisfy one very explicit generality condition are K-stable.
that satisfy one very explicit generality condition are K-stable.