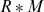26 results
Division algebras and MRD codes from skew polynomials
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 480-500
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 422-427
- Print publication:
- December 2023
-
- Article
- Export citation
FIXED POINTS OF POLYNOMIALS OVER DIVISION RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 01 March 2021, pp. 256-262
- Print publication:
- October 2021
-
- Article
- Export citation
Étale groupoid algebras with coefficients in a sheaf and skew inverse semigroup rings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 07 August 2020, pp. 1592-1626
- Print publication:
- December 2021
-
- Article
- Export citation
HOW A NONASSOCIATIVE ALGEBRA REFLECTS THE PROPERTIES OF A SKEW POLYNOMIAL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 November 2019, pp. 6-26
- Print publication:
- January 2021
-
- Article
- Export citation
NAKAYAMA AUTOMORPHISMS OF ORE EXTENSIONS OVER POLYNOMIAL ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 17 June 2019, pp. 518-530
- Print publication:
- September 2020
-
- Article
- Export citation
LIFTINGS OF A MONOMIAL CURVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 05 July 2018, pp. 230-238
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Zero-divisor Graphs of Ore Extensions Over Reversible Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-805
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation
A Note on Algebras that are Sums of Two Subalgebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-345
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
On a Class of Automaton Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 31-38
-
- Article
- Export citation
SEPARABLY CLOSED FIELDS AND CONTRACTIVE ORE MODULES
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 22 December 2015, pp. 1315-1338
- Print publication:
- December 2015
-
- Article
- Export citation
TRACES ON SEMIGROUP RINGS AND LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 97-118
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
GENERALISED ARMENDARIZ PROPERTIES OF CROSSED PRODUCT TYPE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 313-323
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Jacobson Radicals of Skew Polynomial Rings of Derivation Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 609-613
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
Corrigendum to Example in “Quantum Drinfeld Hecke Algebras“
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, p. 902
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
Quantum Drinfeld Hecke Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 874-901
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
Gröbner bases for quadratic algebras of skew type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 387-401
-
- Article
-
- You have access
- Export citation
GENERALIZED HIGHER DERIVATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 06 January 2012, pp. 266-281
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A UNIFIED APPROACH TO VARIOUS GENERALIZATIONS OF ARMENDARIZ RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 23 February 2010, pp. 361-397
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
ON ANNIHILATOR IDEALS OF SKEW MONOID RINGS*
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 04 December 2009, pp. 161-168
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation

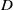
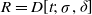
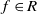
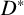
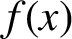
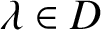
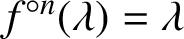
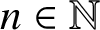
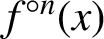
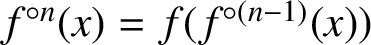
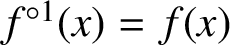
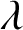
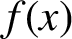
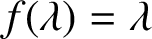

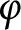
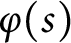
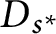
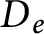
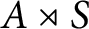

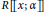

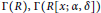
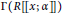
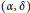



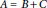
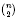 quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM
quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM