We consider the simple random walk on the d-dimensional lattice $\mathbb{Z}^d$ ($d \geq 1$), traveling in potentials which are Bernoulli-distributed. The so-called Lyapunov exponent describes the cost of traveling for the simple random walk in the potential, and it is known that the Lyapunov exponent is strictly monotone in the parameter of the Bernoulli distribution. Hence the aim of this paper is to investigate the effect of the potential on the Lyapunov exponent more precisely, and we derive some Lipschitz-type estimates for the difference between the Lyapunov exponents.

In this paper, we investigate the regularity properties and determine the almost sure multifractal spectrum of a class of random functions constructed as sums of pulses with random dilations and translations. In addition, the continuity moduli of the sample paths of these stochastic processes are investigated.

We prove that any continuous function can be locally approximated at a fixed point $x_{0}$ by an uncountable family resistant to disruptions by the family of continuous functions for which $x_{0}$ is a fixed point. In that context, we also consider the property of quasicontinuity.

We examine dynamical systems which are ‘nonchaotic’ on a big (in the sense of Lebesgue measure) set in each neighbourhood of a fixed point $x_{0}$, that is, the entropy of this system is zero on a set for which $x_{0}$ is a density point. Considerations connected with this family of functions are linked with functions attracting positive entropy at $x_{0}$, that is, each mapping sufficiently close to the function has positive entropy on each neighbourhood of $x_{0}$.

Various properties of continuity for the class of lower semicontinuous convex functions are considered and dual characterizations are established. In particular, it is shown that the restriction of a lower semicontinuous convex function to its domain (respectively, domain of subdifferentiability) is continuous if and only if its subdifferential is strongly cyclically monotone (respectively, σ-cyclically monotone).

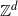
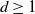
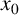
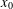
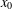
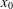
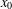
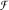The purpose of this paper is to examine which classes of functions from 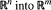can be topologized in a sense that there exist topologies τ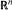1 and τ2 on and 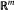respectively, such that 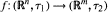is equal to the class C(τ1 , τ2) of all continuous functions . We will show that the Generalized Continuum Hypothesis GCH implies the positive answer for this question for a large number of classes of functions for which the sets {x : f(x) = g(x)} are small in some sense for all f, g ∈ f ≠ g. The topologies will be Hausdorff and connected. It will be also shown that in some model of set theory ZFC with GCH these topologies could be completely regular and Baire. One of the corollaries of this theorem is that GCH implies the existence of a connected Hausdorff topology T on such that the class L of all linear functions g(x) = ax + b coincides with 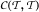. This gives an affirmative answer to a question of Sam Nadler. The above corollary remains true for the class of all polynomials, the class of all analytic functions and the class of all harmonic functions.

We will also prove that several other classes of real functions cannot be topologized. This includes the classes of C∞ functions, differentiable functions, Darboux functions and derivatives.

Let LSC(X) denote the set of extended real valued lower semicontinuous functions on a metrizable space X. If f, f1, f2, f3,... is a sequence in LSC(X), we say 〈fn〉 is epi-convergent to f provided the sequence of epigraphs 〈epi fn〉 is Kuratowski- Painlevé convergent to epi f. In this note we address the following question: what conditions on f and/or on X are necessary and sufficient for this mode of convergence to force epigraphical convergence with respect to the stronger Hausdorff metric and Vietoris topologies?

We give an elementary proof of the theorem of Saks that states that most functions in C[0, 1] have infinite unilateral derivatives at a continuum many points.

We construct an explicit continuous function F such that for each point x, every extended real number is a derived number of F at x and F has an infinite left and an infinite right derived number at x.