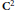15 results
On boundary-non-preserving mappings with Poletsky inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-22
-
- Article
- Export citation
Finely quasiconformal mappings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
Normal families and quasiregular mappings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 79-112
-
- Article
-
- You have access
- HTML
- Export citation
Julia sets of Zorich maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 692-728
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Permutable quasiregular maps
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 105-121
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
Entropy in uniformly quasiregular dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 2397-2427
- Print publication:
- August 2021
-
- Article
- Export citation
SPHERICALIZATION AND FLATTENING PRESERVE UNIFORM DOMAINS IN NONLOCALLY COMPACT METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 February 2020, pp. 68-89
- Print publication:
- February 2022
-
- Article
- Export citation
On slow escaping and non-escaping points of quasimeromorphic mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1190-1216
- Print publication:
- April 2021
-
- Article
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
Poincaré Inequalities and Neumann Problems for the p-Laplacian
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 738-753
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
BOUNDARY ACCESSIBILITY OF A DOMAIN QUASICONFORMALLY EQUIVALENT TO A BALL
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 23 December 2003, pp. 115-118
- Print publication:
- January 2004
-
- Article
- Export citation
PATHWISE CONNECTIVITY OF A CONFORMAL BOUNDARY
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 13 August 2003, pp. 645-650
- Print publication:
- September 2003
-
- Article
- Export citation
Quasiconformal Contactomorphisms and Polynomial Hulls with Convex Fibers
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 5 / 01 October 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 915-935
- Print publication:
- 01 October 1999
-
- Article
-
- You have access
- Export citation

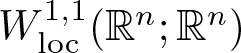






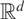
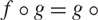
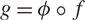
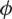
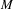

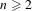
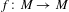
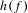
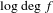
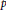
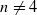 ), then every quasiregular mapping
), then every quasiregular mapping