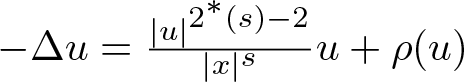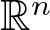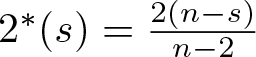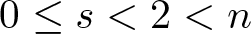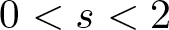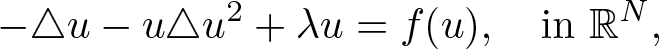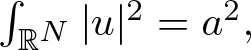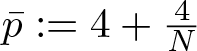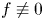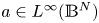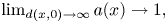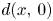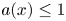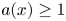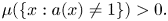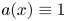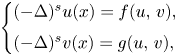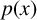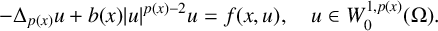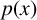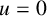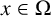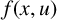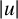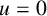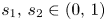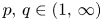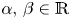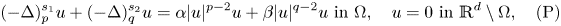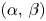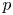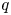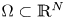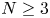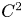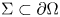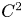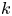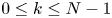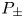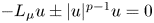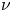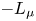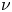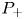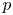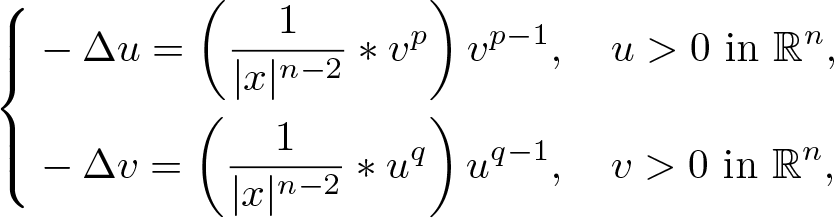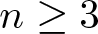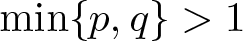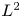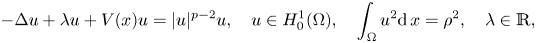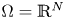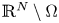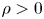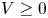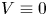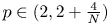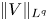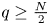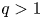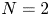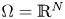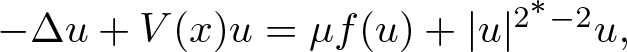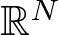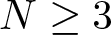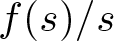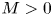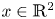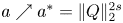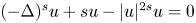124 results
On a perturbed critical semilinear equation with singularity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-35
-
- Article
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 349-387
-
- Article
-
- You have access
- HTML
- Export citation
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 345-374
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
A class of Hessian quotient equations in de Sitter space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 805-821
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Multiplicity of positive solutions for a class of nonhomogeneous elliptic equations in the hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 February 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
On the existence of a nodal solution for p-Laplacian equations depending on the gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 January 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
MULTIPLE SOLUTIONS FOR
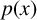 $p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
$p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 346-354
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1-46
-
- Article
-
- You have access
- HTML
- Export citation
Semilinear elliptic equations involving power nonlinearities and Hardy potentials with boundary singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 December 2023, pp. 1-58
-
- Article
- Export citation
LELONG NUMBERS OF m-SUBHARMONIC FUNCTIONS ALONG SUBMANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 1797-1820
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of renormalized solutions to fully anisotropic and inhomogeneous elliptic problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 October 2023, pp. 1-37
-
- Article
- Export citation
On Liouville theorems of a Hartree–Poisson system
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 26 October 2023, pp. 1154-1178
-
- Article
- Export citation
Normalized positive solutions for Schrödinger equations with potentials in unbounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1518-1551
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
A non-periodic indefinite variational problem in ℝN with critical exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 579-612
-
- Article
- Export citation
Radial solvability for Pucci-Lane-Emden systems in annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 494-507
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
COMPACTNESS AND STRUCTURE OF ZERO-STATES FOR UNORIENTED AVILES–GIGA FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 941-982
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Concentration behaviour of normalized ground states of the mass critical fractional Schrödinger equations with ring-shaped potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 1993-2024
- Print publication:
- December 2023
-
- Article
- Export citation