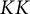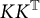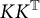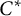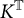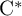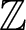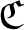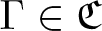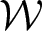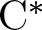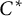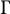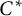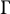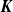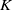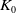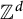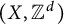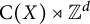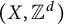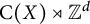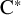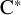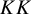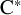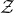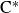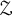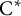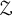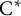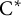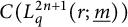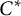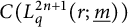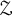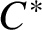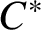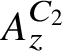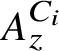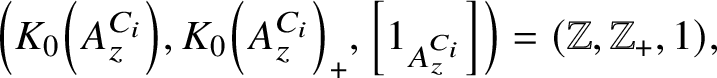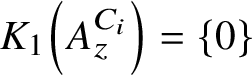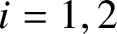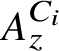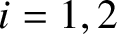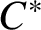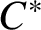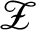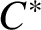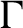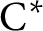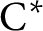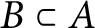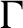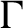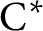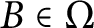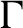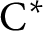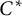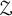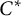81 results
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
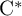 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly outer actions of certain torsion-free amenable groups on the Razak–Jacelon algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 December 2024, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensorially absorbing inclusions of C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of anomalous actions through model action absorption
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial oscillation zero and stable rank one
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2024, pp. 1-68
-
- Article
-
- You have access
- HTML
- Export citation
Unitary groups,
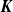 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 229-251
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radius of comparison and mean topological dimension:
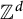 $\mathbb Z^d$-actions
$\mathbb Z^d$-actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 1240-1266
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chaotic tracial dynamics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 May 2023, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random amenable C*-algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On tracial
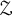 ${\mathcal {Z}}$-stability of simple non-unital
${\mathcal {Z}}$-stability of simple non-unital 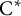 $\mathrm {C}^*$-algebras
$\mathrm {C}^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the classification and description of quantum lens spaces as graph algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 246-282
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colored isomorphism of classifiable C
 $^*$-algebras
$^*$-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 216-245
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonamenable simple
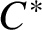 $C^*$
-algebras with tracial approximation
$C^*$
-algebras with tracial approximation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform property
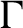 $\Gamma $
for certain
$\Gamma $
for certain
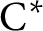 $\mathrm {C^*}$
-algebras
$\mathrm {C^*}$
-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1063-1070
- Print publication:
- December 2022
-
- Article
- Export citation
On one-sided topological conjugacy of topological Markov shifts and gauge actions on Cuntz–Krieger algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 2575-2582
- Print publication:
- August 2022
-
- Article
- Export citation
Regularity of simple nuclear real C*-algebras under tracial conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 139-147
-
- Article
- Export citation
Tracial approximation in simple
 ${C}^{\ast }$
-algebras
${C}^{\ast }$
-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 942-1004
- Print publication:
- August 2022
-
- Article
- Export citation