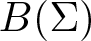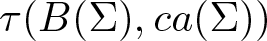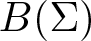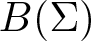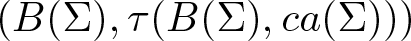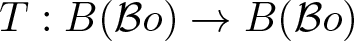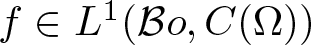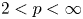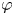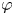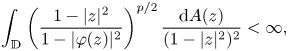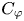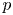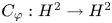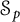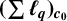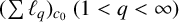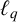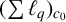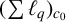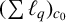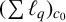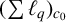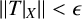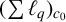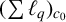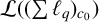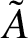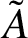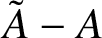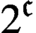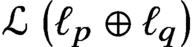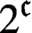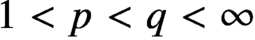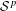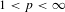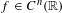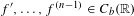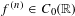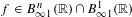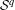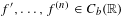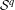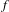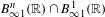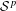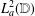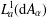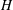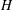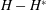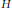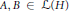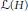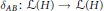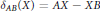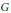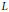32 results
On traces of Bochner representable operators on the space of bounded measurable functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 224-235
-
- Article
-
- You have access
- HTML
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Composition operators on weighted analytic spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 1213-1230
- Print publication:
- December 2023
-
- Article
- Export citation
THE MAXIMAL IDEAL IN THE SPACE OF OPERATORS ON
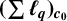 $\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
$\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 21 February 2022, pp. 340-348
- Print publication:
- October 2022
-
- Article
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Banach spaces for which the space of operators has 2𝔠 closed ideals
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 March 2021, e27
-
- Article
-
- You have access
- Open access
- Export citation
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 1993-2016
- Print publication:
- November 2020
-
- Article
- Export citation
Corrigendum to “Generalized Cesàro Matrices”
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, p. 196
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
THE HILBERT–SCHMIDT NORM OF A COMPOSITION OPERATOR ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
CLASSES OF SEQUENTIALLY LIMITED OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 573-586
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
A BOUND FOR SIMILARITY CONDITION NUMBERS OF UNBOUNDED OPERATORS WITH HILBERT–SCHMIDT HERMITIAN COMPONENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 12 September 2014, pp. 331-342
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Schatten p-class property of pseudodifferential operators with symbols in modulation spaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 205 / March 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 119-148
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Generalized D-symmetric Operators II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-27
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
p-VARIATION OF VECTOR MEASURES WITH RESPECT TO BILINEAR MAPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 411-430
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Rearrangement-Invariant Functionals with Applications to Traces on Symmetrically Normed Ideals
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 67-80
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
INTERPOLATION METHODS DEFINED BY MEANS OF POLYGONS AND COMPACT OPERATORS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 3 / October 2007
- Published online by Cambridge University Press:
- 08 January 2008, pp. 653-671
-
- Article
-
- You have access
- Export citation
Preduals and Nuclear Operators Associated with Bounded,
 $p$-Convex,
$p$-Convex, 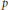 $p$-Concave and Positive
$p$-Concave and Positive 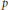 $p$-Summing Operators
$p$-Summing Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 3 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 614-637
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
Classification of Finite Group-Frames and Super-Frames
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 1 / 01 March 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 85-96
- Print publication:
- 01 March 2007
-
- Article
-
- You have access
- Export citation
CYCLES AND 1-UNCONDITIONAL MATRICES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 93 / Issue 3 / November 2006
- Published online by Cambridge University Press:
- 13 October 2006, pp. 761-790
- Print publication:
- November 2006
-
- Article
- Export citation
SOME INTERTWINING RELATIONS MODULO OPERATOR IDEALS
-
- Journal:
- Glasgow Mathematical Journal / Volume 48 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 24 March 2006, pp. 111-117
- Print publication:
- January 2006
-
- Article
-
- You have access
- Export citation