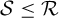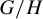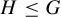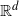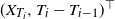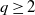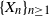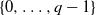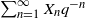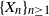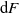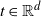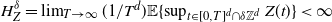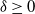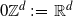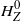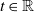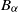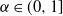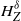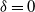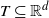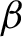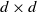165 results
On the strong stability of ergodic iterations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 November 2024, pp. 284-297
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 3385-3427
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Inequalities between time and customer averages for HNB(W)UE arrival processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1199-1219
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Characteristics of the switch process and geometric divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 802-809
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Reliability analyses of linear two-dimensional consecutive k-type systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 14 August 2023, pp. 439-464
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Characterization theorems for pseudo cross-variograms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1219-1231
- Print publication:
- December 2023
-
- Article
- Export citation
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 3707-3725
- Print publication:
- November 2023
-
- Article
- Export citation
Inheritance of strong mixing and weak dependence under renewal sampling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 435-451
- Print publication:
- June 2023
-
- Article
- Export citation
Characterization of random variables with stationary digits
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 August 2022, pp. 931-947
- Print publication:
- December 2022
-
- Article
- Export citation
Kingman’s model with random mutation probabilities: convergence and condensation I
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 25 February 2022, pp. 311-335
- Print publication:
- March 2022
-
- Article
- Export citation
STATIONARY MARKOVIAN ARRIVAL PROCESSES: RESULTS AND OPEN PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 54-68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A stochastic process on a network with connections to Laplacian systems of equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 21 January 2022, pp. 254-278
- Print publication:
- March 2022
-
- Article
- Export citation
On the continuity of Pickands constants
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 187-201
- Print publication:
- March 2022
-
- Article
- Export citation
Long range dependence of heavy-tailed random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 569-593
- Print publication:
- September 2021
-
- Article
- Export citation
Invariant densities for random systems of the interval
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 141-179
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
Markov chains with exponential return times are finitary
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 2918-2926
- Print publication:
- October 2021
-
- Article
- Export citation
Ergodicity of affine processes on the cone of symmetric positive semidefinite matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 825-854
- Print publication:
- September 2020
-
- Article
- Export citation
Central limit theorems for nearly long range dependent subordinated linear processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 637-656
- Print publication:
- June 2020
-
- Article
- Export citation