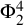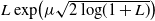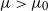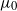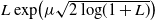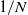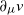79 results
Single-item continuous-review inventory models with random supplies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 134-170
- Print publication:
- March 2025
-
- Article
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Super-replication of life-contingent options under the Black–Scholes framework
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1263-1277
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 465-489
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Duality theory for exponential utility-based hedging in the Almgren–Chriss model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 420-438
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
PRICING AND HEDGING OF VIX DERIVATIVES IN MODIFIED STOCHASTIC MODELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 June 2023, pp. 351-352
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Measuring the suboptimality of dividend controls in a Brownian risk model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1442-1472
- Print publication:
- December 2023
-
- Article
- Export citation
Optimal stopping under g-Expectation with
 ${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$
-integrable reward process
${L}\exp\bigl(\mu\sqrt{2\log\!(1+\textbf{L})}\bigr)$
-integrable reward process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 September 2022, pp. 241-252
- Print publication:
- March 2023
-
- Article
- Export citation
Optimal multiple stopping problem under nonlinear expectation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 151-178
- Print publication:
- March 2023
-
- Article
- Export citation
Rate of convergence for particle approximation of PDEs in Wasserstein space
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 28 July 2022, pp. 992-1008
- Print publication:
- December 2022
-
- Article
- Export citation
Extended reduced-form framework for non-life insurance
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 945-973
- Print publication:
- September 2022
-
- Article
- Export citation
Optimal consumption with Hindy–Huang–Kreps preferences under nonlinear expectations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1222-1251
- Print publication:
- December 2022
-
- Article
- Export citation
Zipf’s law for atlas models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1276-1297
- Print publication:
- December 2020
-
- Article
- Export citation
Skeletal stochastic differential equations for superprocesses
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 23 November 2020, pp. 1111-1134
- Print publication:
- December 2020
-
- Article
- Export citation
Solving the 4NLS with white noise initial data
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 18 November 2020, e48
-
- Article
-
- You have access
- Open access
- Export citation
Mean square rate of convergence for random walk approximation of forward-backward SDEs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 735-771
- Print publication:
- September 2020
-
- Article
- Export citation
Two results on dynamic extensions of deviation measures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 531-540
- Print publication:
- June 2020
-
- Article
- Export citation
Skeletal stochastic differential equations for continuous-state branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1122-1150
- Print publication:
- December 2019
-
- Article
- Export citation
Semi-static variance-optimal hedging in stochastic volatility models with Fourier representation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 787-809
- Print publication:
- September 2019
-
- Article
- Export citation
STOCHASTIC NONLINEAR SCHRÖDINGER EQUATION WITH ALMOST SPACE–TIME WHITE NOISE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 21 June 2019, pp. 44-67
- Print publication:
- August 2020
-
- Article
- Export citation