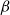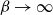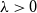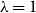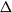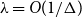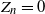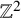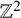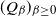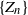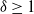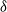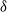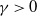301 results
The speed of a biased walk on a Galton–Watson tree without leaves is monotonic for low values of bias
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 05 March 2025, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Phase-type representations for exponential distributions
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-31
-
- Article
- Export citation
Critical configurations of the hard-core model on square grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 04 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Sampling from the random cluster model on random regular graphs at all temperatures via Glauber dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Optimal mixing via tensorization for random independent sets on arbitrary trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 259-275
-
- Article
-
- You have access
- HTML
- Export citation
Regeneration of branching processes with immigration in varying environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 422-444
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Completion problems and sparsity for Kemeny’s constant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-18
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficiency of reversible MCMC methods: elementary derivations and applications to composite methods
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 188-208
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Maximizing the probability of visiting a set infinitely often for a Markov decision process with Borel state and action spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 August 2024, pp. 1424-1447
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recurrence and transience of a Markov chain on
 $\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
$\mathbb Z$+ and evaluation of prior distributions for a Poisson mean
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 1361-1379
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Perfect sampling of stochastic matching models with reneging
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1307-1339
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
A subgeometric convergence formula for finite-level M/G/1-type Markov chains: via a block-decomposition-friendly solution to the Poisson equation of the deviation matrix
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 389-429
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
An inaccuracy measure between non-explosive point processes with applications to Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 735-756
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Collapse and diffusion in harmonic activation and transport
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
R-positivity and the existence of zero-temperature limits of Gibbs measures on nearest-neighbor matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 558-577
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Branching processes in random environments with thresholds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 495-544
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Disparity-persistence and the multistep friendship paradox
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 July 2023, pp. 290-298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sensitivity of mixing times of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 18 July 2023, pp. 1400-1431
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributions of random variables involved in discrete censored δ-shock models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1144-1170
- Print publication:
- December 2023
-
- Article
- Export citation