The Ceresa cycle is an algebraic cycle attached to a smooth algebraic curve with a marked point, which is trivial when the curve is hyperelliptic with a marked Weierstrass point. The image of the Ceresa cycle under a certain cycle class map provides a class in étale cohomology called the Ceresa class. Describing the Ceresa class explicitly for nonhyperelliptic curves is in general not easy. We present a ‘combinatorialization’ of this problem, explaining how to define a Ceresa class for a tropical algebraic curve and also for a topological surface endowed with a multiset of commuting Dehn twists (where it is related to the Morita cocycle on the mapping class group). We explain how these are related to the Ceresa class of a smooth algebraic curve over $\mathbb {C}(\!(t)\!)$ and show that the Ceresa class in each of these settings is torsion.

We introduce the notion of refined unramified cohomology of algebraic schemes and prove comparison theorems that identify some of these groups with cycle groups. This generalizes to cycles of arbitrary codimension previous results of Bloch–Ogus, Colliot-Thélène–Voisin, Kahn, Voisin, and Ma. We combine our approach with the Bloch–Kato conjecture, proven by Voevodsky, to show that on a smooth complex projective variety, any homologically trivial torsion cycle with trivial Abel–Jacobi invariant has coniveau $1$. This establishes a torsion version of a conjecture of Jannsen originally formulated $\otimes \mathbb {Q}$. We further show that the group of homologically trivial torsion cycles modulo algebraic equivalence has a finite filtration (by coniveau) such that the graded quotients are determined by higher Abel–Jacobi invariants that we construct. This may be seen as a variant for torsion cycles modulo algebraic equivalence of a conjecture of Green. We also prove $\ell$-adic analogues of these results over any field $k$ which contains all $\ell$-power roots of unity.

We prove an extension of the Kato–Saito unramified class field theory for smooth projective schemes over a finite field to a class of normal projective schemes. As an application, we obtain Bloch’s formula for the Chow groups of $0$-cycles on such schemes. We identify the Chow group of $0$-cycles on a normal projective scheme over an algebraically closed field to the Suslin homology of its regular locus. Our final result is a Roitman torsion theorem for smooth quasiprojective schemes over algebraically closed fields. This completes the missing p-part in the torsion theorem of Spieß and Szamuely.

Consider three normalized cuspidal eigenforms of weight $2$ and prime level p. Under the assumption that the global root number of the associated triple product L-function is $+1$ , we prove that the complex Abel–Jacobi image of the modified diagonal cycle of Gross–Kudla–Schoen on the triple product of the modular curve $X_0(p)$ is torsion in the corresponding Hecke isotypic component of the Griffiths intermediate Jacobian. The same result holds with the complex Abel–Jacobi map replaced by its étale counterpart. As an application, we deduce torsion properties of Chow–Heegner points associated with modified diagonal cycles on elliptic curves of prime conductor with split multiplicative reduction. The approach also works in the case of composite square-free level.

This article is about Lehn–Lehn–Sorger–van Straten eightfolds $Z$ and their anti-symplectic involution $\iota$. When $Z$ is birational to the Hilbert scheme of points on a K3 surface, we give an explicit formula for the action of $\iota$ on the Chow group of $0$-cycles of $Z$. The formula is in agreement with the Bloch–Beilinson conjectures and has some non-trivial consequences for the Chow ring of the quotient.

We show that the additive higher Chow groups of regular schemes over a field induce a Zariski sheaf of pro-differential graded algebras, the Milnor range of which is isomorphic to the Zariski sheaf of big de Rham–Witt complexes. This provides an explicit cycle-theoretic description of the big de Rham–Witt sheaves. Several applications are derived.

We consider Calabi–Yau n-folds X arising from certain hyperplane arrangements. Using Fu–Vial’s theory of distinguished cycles for varieties with motive of abelian type, we show that the subring of the Chow ring of X generated by divisors, Chern classes and intersections of subvarieties of positive codimension injects into cohomology. We also prove Voisin’s conjecture for X, and Voevodsky’s smash-nilpotence conjecture for odd-dimensional X.

The Beauville–Voisin conjecture for a hyperkähler manifold $X$ states that the subring of the Chow ring $A^{\ast }(X)$ generated by divisor classes and Chern characters of the tangent bundle injects into the cohomology ring of $X$. We prove a weak version of this conjecture when $X$ is the Hilbert scheme of points on a K3 surface for the subring generated by divisor classes and tautological classes. This in particular implies the weak splitting conjecture of Beauville for these geometries. In the process, we extend Lehn’s formula and the Li–Qin–Wang $W_{1+\infty }$ algebra action from cohomology to Chow groups for the Hilbert scheme of an arbitrary smooth projective surface $S$.

We study special cycles on a Shimura variety of orthogonal type over a totally real field of degree d associated with a quadratic form in $n+2$ variables whose signature is $(n,2)$ at e real places and $(n+2,0)$ at the remaining $d-e$ real places for $1\leq e <d$. Recently, these cycles were constructed by Kudla and Rosu–Yott, and they proved that the generating series of special cycles in the cohomology group is a Hilbert-Siegel modular form of half integral weight. We prove that, assuming the Beilinson–Bloch conjecture on the injectivity of the higher Abel–Jacobi map, the generating series of special cycles of codimension er in the Chow group is a Hilbert–Siegel modular form of genus r and weight $1+n/2$. Our result is a generalization of Kudla’s modularity conjecture, solved by Yuan–Zhang–Zhang unconditionally when $e=1$.

We prove that a Küchle fourfold $X$ of type 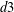d3 has a multiplicative Chow–Künneth decomposition. We present some consequences for the Chow ring of $X$.

Given a smooth variety $X$ and an effective Cartier divisor $D\subset X$, we show that the cohomological Chow group of 0-cycles on the double of $X$ along $D$ has a canonical decomposition in terms of the Chow group of 0-cycles $\text{CH}_{0}(X)$ and the Chow group of 0-cycles with modulus $\text{CH}_{0}(X|D)$ on $X$. When $X$ is projective, we construct an Albanese variety with modulus and show that this is the universal regular quotient of $\text{CH}_{0}(X|D)$. As a consequence of the above decomposition, we prove the Roitman torsion theorem for the 0-cycles with modulus. We show that $\text{CH}_{0}(X|D)$ is torsion-free and there is an injective cycle class map $\text{CH}_{0}(X|D){\hookrightarrow}K_{0}(X,D)$ if $X$ is affine. For a smooth affine surface $X$, this is strengthened to show that $K_{0}(X,D)$ is an extension of $\text{CH}_{1}(X|D)$ by $\text{CH}_{0}(X|D)$.

In this paper, motivated by a problem posed by Barry Mazur, we show that for smooth projective varieties over the rationals, the odd cohomology groups of degree less than or equal to the dimension can be modeled by the cohomology of an abelian variety, provided the geometric coniveau is maximal. This provides an affirmative answer to Mazur’s question for all uni-ruled threefolds, for instance. Concerning cohomology in degree three, we show that the image of the Abel–Jacobi map admits a distinguished model over the rationals.

We formulate a conjectural hard Lefschetz property for Chow groups and prove it in some special cases, roughly speaking, for varieties with finite-dimensional motive, and for varieties whose self-product has vanishing middle-dimensional Griõths group. An appendix includes related statements that follow from results of Vial.

Let τ be the involution changing the sign of two coordinates in ℙ4. We prove that τ induces the identity action on the second Chow group of the intersection of a τ-invariant cubic with a τ-invariant quadric hypersurface in ℙ4. Let lτ and Πτ be the one- and two-dimensional components of the fixed locus of the involution τ. We describe the generalized Prymian associated with the projection of a τ-invariant cubic 𝓵 ⊂ P4 from lτ onto Πτ in terms of the Prymians 𝓅2 and 𝓅3 associated with the double covers of two irreducible components, of degree 2 and 3, respectively, of the reducible discriminant curve. This gives a precise description of the induced action of the involution τ on the continuous part of the Chow group CH2 (𝓵). The action on the subgroup corresponding to 𝓅3 is the identity, and the action on the subgroup corresponding to 𝓅2 is the multiplication by —1.

We consider étale motivic or Lichtenbaum cohomology and its relation to algebraic cycles. We give an geometric interpretation of Lichtenbaum cohomology and use it to show that the usual integral cycle maps extend to maps on integral Lichtenbaum cohomology. We also show that Lichtenbaum cohomology, in contrast to the usual motivic cohomology, compares well with integral cohomology theories. For example, we formulate integral étale versions of the Hodge and the Tate conjecture, and show that these are equivalent to the usual rational conjectures.

We prove that every curve on a separably rationally connected variety is rationally equivalent to a (non-effective) integral sum of rational curves. That is, the Chow group of 1-cycles is generated by rational curves. Applying the same technique, we also show that the Chow group of 1-cycles on a separably rationally connected Fano complete intersection of index at least 2 is generated by lines. As a consequence, we give a positive answer to a question of Professor Totaro about integral Hodge classes on rationally connected 3-folds. And by a result of Professor Voisin, the general case is a consequence of the Tate conjecture for surfaces over finite fields.

In this work, we s uggest a defnition for the category of mixed motives generated by the motive h1 (E) for E an elliptic curve without complex multiplication. We then compute the cohomology of this category. Modulo a strengthening of the Beilinson-Soulé conjecture, we show that the cohomology of our category agrees with the expected motivic cohomology groups. Finally for each pure motive (Symnh1 (E)) (–1) we construct families of nontrivial motives whose highest associated weight graded piece is (Symnh1 (E)) (–1).

Voevodsky conjectured that numerical equivalence and smash equivalence coincide on a smooth projective variety. We prove the conjecture for 1-cycles on varieties dominated by products of curves.

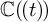
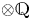
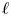
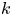
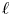
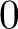
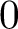
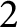
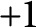
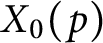
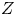
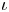
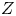
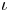
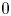
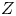
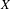
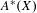
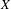
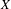
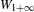
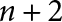
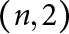
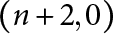
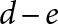
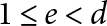
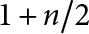
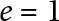
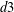
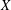
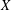
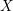
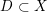
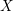
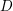
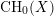
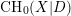
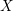
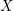
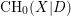
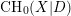
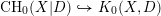
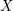
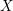
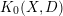
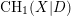
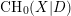
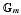We address the question of lifting the étale unipotent fundamental group of curves to the level of algebraic cycles and show that a sequence of algebraic cycles whose sum satisfies the Maurer-Cartan equation would do the job. For any elliptic curve with the origin removed and the curve , we construct such a sequence of algebraic cycles whose image under the cycle map gives rise to the étale unipotent fundamental group of the curve.