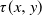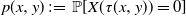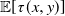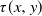149 results
2 - Probabilistic Methods in Arbitrage Pricing
-
- Book:
- Theoretical Foundations of Asset Pricing
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 42-105
-
- Chapter
- Export citation
8 - Other Fine Topologies
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 114-136
-
- Chapter
- Export citation
6 - Mathematical Modelling and Simulation: Diffusion-Based Molecular Communication
-
- Book:
- Molecular Communication
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 92-118
-
- Chapter
- Export citation
Discounted optimal stopping zero-sum games in diffusion type models with maxima and minima
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 December 2024, pp. 241-270
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundary crossing problems and functional transformations for Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 October 2024, pp. 395-421
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Optimal drift rate control and two-sided impulse control for a Brownian system with the long-run average criterion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 271-304
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
De Finetti’s control problem with a concave bound on the control rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 January 2024, pp. 834-850
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - Elements of Stochastic Mechanics of Transport
-
- Book:
- Physicochemical Mechanics
- Published online:
- 30 November 2023
- Print publication:
- 14 December 2023, pp 36-56
-
- Chapter
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
2 - War and the Culture of Politeness
-
- Book:
- Multiphase Flow with Solid Particles
- Published online:
- 05 October 2023
- Print publication:
- 19 October 2023, pp 6-43
-
- Chapter
- Export citation
Stochastic ordering results on the duration of the gambler’s ruin game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 603-621
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
2 - Dynamical Systems and Markov Processes
- from Part I - Concepts from Modeling, Inference, and Computing
-
- Book:
- Data Modeling for the Sciences
- Published online:
- 17 August 2023
- Print publication:
- 31 August 2023, pp 40-107
-
- Chapter
- Export citation
ON THE EXPECTED UNIFORM ERROR OF BROWNIAN MOTION APPROXIMATED BY THE LÉVY–CIESIELSKI CONSTRUCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 581-593
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
5 - Coupling Regimes for Multiphase Flow
-
- Book:
- Fluid Dynamics of Particles, Drops, and Bubbles
- Published online:
- 28 July 2023
- Print publication:
- 17 August 2023, pp 192-221
-
- Chapter
- Export citation
An elementary approach to the inverse first-passage-time problem for soft-killed Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 279-300
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
A first-passage-place problem for integrated diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 55-67
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
7 - Dynamics
-
- Book:
- Physics of Charged Macromolecules
- Published online:
- 16 February 2023
- Print publication:
- 23 February 2023, pp 196-278
-
- Chapter
- Export citation
On the splitting and aggregating of Hawkes processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 676-692
- Print publication:
- June 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Stochastic Processes
-
- Book:
- The Statistical Mechanics of Irreversible Phenomena
- Published online:
- 14 July 2022
- Print publication:
- 28 July 2022, pp 147-201
-
- Chapter
- Export citation