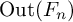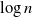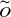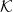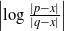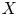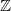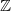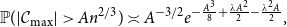180 results
First-passage time for Sinai’s random walk in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 29 November 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
3 - Influential Observations
-
- Book:
- Ethics in Econometrics
- Published online:
- 14 November 2024
- Print publication:
- 28 November 2024, pp 54-87
-
- Chapter
- Export citation
7 - Spurious Relations
-
- Book:
- Ethics in Econometrics
- Published online:
- 14 November 2024
- Print publication:
- 28 November 2024, pp 161-185
-
- Chapter
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Topics in representation theory of finite groups
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 1-86
-
- Chapter
- Export citation

Harmonic Functions and Random Walks on Groups
-
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024
Scaling limit of the local time of random walks conditioned to stay positive
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 February 2024, pp. 1060-1074
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Diffusion of H2O in Smectite Gels: Obstruction Effects of Bound H2O Layers
-
- Journal:
- Clays and Clay Minerals / Volume 51 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 01 January 2024, pp. 9-22
-
- Article
-
- You have access
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strong convergence of an epidemic model with mixing groups
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 430-463
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
4 - Molecular Diffusion
-
- Book:
- An Introduction to Solute Transport in Heterogeneous Geologic Media
- Published online:
- 02 February 2023
- Print publication:
- 09 February 2023, pp 93-122
-
- Chapter
- Export citation
Toward random walk-based clustering of variable-order networks
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 22 December 2022, pp. 381-399
-
- Article
- Export citation
An elementary approach to component sizes in critical random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 11 November 2022, pp. 1228-1242
- Print publication:
- December 2022
-
- Article
- Export citation
John’s walk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 November 2022, pp. 473-491
- Print publication:
- June 2023
-
- Article
- Export citation
Central limit theorems for counting measures in coarse negative curvature
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1980-2013
- Print publication:
- October 2022
-
- Article
- Export citation
Coexistence of lazy frogs on
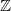 ${\mathbb{Z}}$
${\mathbb{Z}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 702-713
- Print publication:
- September 2022
-
- Article
- Export citation
Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 840-869
-
- Article
- Export citation
8 - Applications
- from Part III - Discrete Functional Analysis
-
- Book:
- Classical and Discrete Functional Analysis with Measure Theory
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022, pp 333-402
-
- Chapter
- Export citation
4 - Overview of Mathematical Tools
- from Part I - Fundamentals
-
- Book:
- Electronic Sensor Design Principles
- Published online:
- 23 December 2021
- Print publication:
- 06 January 2022, pp 189-235
-
- Chapter
- Export citation
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation