Given graphs G and H, a family of vertex-disjoint copies of H in G is called an H-tiling. Conlon, Gowers, Samotij and Schacht showed that for a given graph H and a constant γ>0, there exists C>0 such that if $p \ge C{n^{ - 1/{m_2}(H)}}$ , then asymptotically almost surely every spanning subgraph G of the random graph 𝒢(n, p) with minimum degree at least

$\delta (G) \ge (1 - \frac{1}{{{\chi _{{\rm{cr}}}}(H)}} + \gamma )np$

$\gamma {(C/p)^{{m_2}(H)}}$

$p \ge C{n^{ - 1/{m_2}(H)}}$

Let m(k) denote the maximum number of edges in a non-extendable, intersecting k-graph. Erdős and Lovász proved that m(k) ≤ kk. For k ≥ 625 we prove m(k) < kk・e−k1/4/6.

We study a restricted form of list colouring, for which every pair of lists that correspond to adjacent vertices may not share more than one colour. The optimal list size such that a proper list colouring is always possible given this restriction, we call separation choosability. We show for bipartite graphs that separation choosability increases with (the logarithm of) the minimum degree. This strengthens results of Molloy and Thron and, partially, of Alon. One attempt to drop the bipartiteness assumption precipitates a natural class of Ramsey-type questions, of independent interest. For example, does every triangle-free graph of minimum degree d contain a bipartite induced subgraph of minimum degree Ω(log d) as d→∞?

We prove that the number of multigraphs with vertex set {1, . . ., n} such that every four vertices span at most nine edges is an2+o(n2) where a is transcendental (assuming Schanuel's conjecture from number theory). This is an easy consequence of the solution to a related problem about maximizing the product of the edge multiplicities in certain multigraphs, and appears to be the first explicit (somewhat natural) question in extremal graph theory whose solution is transcendental. These results may shed light on a question of Razborov, who asked whether there are conjectures or theorems in extremal combinatorics which cannot be proved by a certain class of finite methods that include Cauchy–Schwarz arguments.

Our proof involves a novel application of Zykov symmetrization applied to multigraphs, a rather technical progressive induction, and a straightforward use of hypergraph containers.

For fixed integers p and q, let f(n,p,q) denote the minimum number of colours needed to colour all of the edges of the complete graph Kn such that no clique of p vertices spans fewer than q distinct colours. Any edge-colouring with this property is known as a (p,q)-colouring. We construct an explicit (5,5)-colouring that shows that f(n,5,5) ≤ n1/3 + o(1) as n → ∞. This improves upon the best known probabilistic upper bound of O(n1/2) given by Erdős and Gyárfás, and comes close to matching the best known lower bound Ω(n1/3).

The total distance (or Wiener index) of a connected graph $G$ is the sum of all distances between unordered pairs of vertices of $G$. DeLaViña and Waller [‘Spanning trees with many leaves and average distance’, Electron. J. Combin.15(1) (2008), R33, 14 pp.] conjectured in 2008 that if $G$ has diameter $D>2$ and order $2D+1$, then the total distance of $G$ is at most the total distance of the cycle of the same order. In this note, we prove that this conjecture is true for 2-connected graphs.

We consider distance colourings in graphs of maximum degree at most d and how excluding one fixed cycle of length ℓ affects the number of colours required as d → ∞. For vertex-colouring and t ⩾ 1, if any two distinct vertices connected by a path of at most t edges are required to be coloured differently, then a reduction by a logarithmic (in d) factor against the trivial bound O(dt) can be obtained by excluding an odd cycle length ℓ ⩾ 3t if t is odd or by excluding an even cycle length ℓ ⩾ 2t + 2. For edge-colouring and t ⩾ 2, if any two distinct edges connected by a path of fewer than t edges are required to be coloured differently, then excluding an even cycle length ℓ ⩾ 2t is sufficient for a logarithmic factor reduction. For t ⩾ 2, neither of the above statements are possible for other parity combinations of ℓ and t. These results can be considered extensions of results due to Johansson (1996) and Mahdian (2000), and are related to open problems of Alon and Mohar (2002) and Kaiser and Kang (2014).

Two graphs G1 and G2 on n vertices are said to pack if there exist injective mappings of their vertex sets into [n] such that the images of their edge sets are disjoint. A longstanding conjecture due to Bollobás and Eldridge and, independently, Catlin, asserts that if (Δ(G1) + 1)(Δ(G2) + 1) ⩽ n + 1, then G1 and G2 pack. We consider the validity of this assertion under the additional assumption that G1 or G2 has bounded codegree. In particular, we prove for all t ⩾ 2 that if G1 contains no copy of the complete bipartite graph K2,t and Δ(G1) > 17t · Δ(G2), then (Δ(G1) + 1)(Δ(G2) + 1) ⩽ n + 1 implies that G1 and G2 pack. We also provide a mild improvement if moreover G2 contains no copy of the complete tripartite graph K1,1,s, s ⩾ 1.

An oriented k-uniform hypergraph (a family of ordered k-sets) has the ordering property (or Property O) if, for every linear order of the vertex set, there is some edge oriented consistently with the linear order. We find bounds on the minimum number of edges in a hypergraph with Property O.

An r-uniform hypergraph is called an r-graph. A hypergraph is linear if every two edges intersect in at most one vertex. Given a linear r-graph H and a positive integer n, the linear Turán number exL(n,H) is the maximum number of edges in a linear r-graph G that does not contain H as a subgraph. For each ℓ ≥ 3, let Crℓ denote the r-uniform linear cycle of length ℓ, which is an r-graph with edges e1, . . ., eℓ such that, for all i ∈ [ℓ−1], |ei ∩ ei+1|=1, |eℓ ∩ e1|=1 and ei ∩ ej = ∅ for all other pairs {i,j}, i ≠ j. For all r ≥ 3 and ℓ ≥ 3, we show that there exists a positive constant c = cr,ℓ, depending only r and ℓ, such that exL(n,Crℓ) ≤ cn1+1/⌊ℓ/2⌋. This answers a question of Kostochka, Mubayi and Verstraëte [30]. For even ℓ, our result extends the result of Bondy and Simonovits [7] on the Turán numbers of even cycles to linear hypergraphs.

Using our results on linear Turán numbers, we also obtain bounds on the cycle-complete hypergraph Ramsey numbers. We show that there are positive constants a = am,r and b = bm,r, depending only on m and r, such that

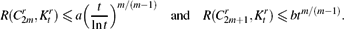\begin{equation} R(C^r_{2m}, K^r_t)\leq a \Bigl(\frac{t}{\ln t}\Bigr)^{{m}/{(m-1)}} \quad\text{and}\quad R(C^r_{2m+1}, K^r_t)\leq b t^{{m}/{(m-1)}}. \end{equation}

Given hypergraphs F and H, an F-factor in H is a set of vertex-disjoint copies of F which cover all the vertices in H. Let K−4 denote the 3-uniform hypergraph with four vertices and three edges. We show that for sufficiently large n ∈ 4ℕ, every 3-uniform hypergraph H on n vertices with minimum codegree at least n/2−1 contains a K−4-factor. Our bound on the minimum codegree here is best possible. It resolves a conjecture of Lo and Markström [15] for large hypergraphs, who earlier proved an asymptotically exact version of this result. Our proof makes use of the absorbing method as well as a result of Keevash and Mycroft [11] concerning almost perfect matchings in hypergraphs.

For an orientation H with n vertices, let T(H) denote the maximum possible number of labelled copies of H in an n-vertex tournament. It is easily seen that T(H) ≥ n!/2e(H), as the latter is the expected number of such copies in a random tournament. For n odd, let R(H) denote the maximum possible number of labelled copies of H in an n-vertex regular tournament. In fact, Adler, Alon and Ross proved that for H=Cn, the directed Hamilton cycle, T(Cn) ≥ (e−o(1))n!/2n, and it was observed by Alon that already R(Cn) ≥ (e−o(1))n!/2n. Similar results hold for the directed Hamilton path Pn. In other words, for the Hamilton path and cycle, the lower bound derived from the expectation argument can be improved by a constant factor. In this paper we significantly extend these results, and prove that they hold for a larger family of orientations H which includes all bounded-degree Eulerian orientations and all bounded-degree balanced orientations, as well as many others. One corollary of our method is that for any fixed k, every k-regular orientation H with n vertices satisfies T(H) ≥ (ek−o(1))n!/2e(H), and in fact, for n odd, R(H) ≥ (ek−o(1))n!/2e(H).

Given a family of r-uniform hypergraphs ${\cal F}$ (or r-graphs for brevity), the Turán number ex(n,${\cal F})$ of ${\cal F}$ is the maximum number of edges in an r-graph on n vertices that does not contain any member of ${\cal F}$. A pair {u,v} is covered in a hypergraph G if some edge of G contains {u, v}. Given an r-graph F and a positive integer p ⩾ n(F), where n(F) denotes the number of vertices in F, let HFp denote the r-graph obtained as follows. Label the vertices of F as v1,. . .,vn(F). Add new vertices vn(F)+1,. . .,vp. For each pair of vertices vi, vj not covered in F, add a set Bi,j of r − 2 new vertices and the edge {vi, vj} ∪ Bi,j, where the Bi,j are pairwise disjoint over all such pairs {i, j}. We call HFp the expanded p-clique with an embedded F. For a relatively large family of F, we show that for all sufficiently large n, ex(n,HFp) = |Tr(n, p − 1)|, where Tr(n, p − 1) is the balanced complete (p − 1)-partite r-graph on n vertices. We also establish structural stability of near-extremal graphs. Our results generalize or strengthen several earlier results and provide a class of hypergraphs for which the Turán number is exactly determined (for large n).

Given a graph F, let st(F) be the number of subdivisions of F, each with a different vertex set, which one can guarantee in a graph G in which every edge lies in at least t copies of F. In 1990, Tuza asked for which graphs F and large t, one has that st(F) is exponential in a power of t. We show that, somewhat surprisingly, the only such F are complete graphs, and for every F which is not complete, st(F) is polynomial in t. Further, for a natural strengthening of the local condition above, we also characterize those F for which st(F) is exponential in a power of t.

We study the lower tail large deviation problem for subgraph counts in a random graph. Let XH denote the number of copies of H in an Erdős–Rényi random graph $\mathcal{G}(n,p)$. We are interested in estimating the lower tail probability $\mathbb{P}(X_H \le (1-\delta) \mathbb{E} X_H)$ for fixed 0 < δ < 1.

Thanks to the results of Chatterjee, Dembo and Varadhan, this large deviation problem has been reduced to a natural variational problem over graphons, at least for p ≥ n−αH (and conjecturally for a larger range of p). We study this variational problem and provide a partial characterization of the so-called ‘replica symmetric’ phase. Informally, our main result says that for every H, and 0 < δ < δH for some δH > 0, as p → 0 slowly, the main contribution to the lower tail probability comes from Erdős–Rényi random graphs with a uniformly tilted edge density. On the other hand, this is false for non-bipartite H and δ close to 1.

We consider the Widom–Rowlinson model of two types of interacting particles on d-regular graphs. We prove a tight upper bound on the occupancy fraction, the expected fraction of vertices occupied by a particle under a random configuration from the model. The upper bound is achieved uniquely by unions of complete graphs on d + 1 vertices, Kd+1. As a corollary we find that Kd+1 also maximizes the normalized partition function of the Widom–Rowlinson model over the class of d-regular graphs. A special case of this shows that the normalized number of homomorphisms from any d-regular graph G to the graph HWR, a path on three vertices with a loop on each vertex, is maximized by Kd+1. This proves a conjecture of Galvin.

If n ⩾ k + 1 and G is a connected n-vertex graph, then one can add $\binom{k}{2}$ edges to G so that the resulting graph contains the complete graph Kk+1. This yields that for any connected graph G with at least k + 1 vertices, one can add $\binom{k}{2}$ edges to G so that the resulting graph has chromatic number > k. A long time ago, Bollobás suggested that for every k ⩾ 3 there exists a k-chromatic graph Gk such that after adding to it any $\binom{k}{2}$ − 1 edges, the chromatic number of the resulting graph is still k. In this note we prove this conjecture.

We give several results showing that different discrete structures typically gain certain spanning substructures (in particular, Hamilton cycles) after a modest random perturbation. First, we prove that adding linearly many random edges to a dense k-uniform hypergraph ensures the (asymptotically almost sure) existence of a perfect matching or a loose Hamilton cycle. The proof involves an interesting application of Szemerédi's Regularity Lemma, which might be independently useful. We next prove that digraphs with certain strong expansion properties are pancyclic, and use this to show that adding a linear number of random edges typically makes a dense digraph pancyclic. Finally, we prove that perturbing a certain (minimum-degree-dependent) number of random edges in a tournament typically ensures the existence of multiple edge-disjoint Hamilton cycles. All our results are tight.

We give an easy method for constructing containers for simple hypergraphs. The method also has consequences for non-simple hypergraphs. Some applications are given; in particular, a very transparent calculation is offered for the number of H-free hypergraphs, where H is some fixed uniform hypergraph.

The total irregularity of a simple undirected graph $G$ is defined as $\text{irr}_{t}(G)=\frac{1}{2}\sum _{u,v\in V(G)}|d_{G}(u)-d_{G}(v)|$, where $d_{G}(u)$ denotes the degree of a vertex $u\in V(G)$. Obviously, $\text{irr}_{t}(G)=0$ if and only if $G$ is regular. Here, we characterise the nonregular graphs with minimal total irregularity and thereby resolve the recent conjecture by Zhu et al. [‘The minimal total irregularity of graphs’, Preprint, 2014, arXiv:1404.0931v1 ] about the lower bound on the minimal total irregularity of nonregular connected graphs. We show that the conjectured lower bound of $2n-4$ is attained only if nonregular connected graphs of even order are considered, while the sharp lower bound of $n-1$ is attained by graphs of odd order. We also characterise the nonregular graphs with the second and the third smallest total irregularity.