Contents
Research Article
Graphs with Maximal Even Girth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 915-934
-
- Article
-
- You have access
- Export citation
On a Transformation Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 935-941
-
- Article
-
- You have access
- Export citation
Some Results Relating the Behaviour of Fourier Transforms Near the Origin and at Infinity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 942-950
-
- Article
-
- You have access
- Export citation
A Summation Formula Involving σk(n), k > 1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 951-964
-
- Article
-
- You have access
- Export citation
Finite Groups whose Powers have no Countably Infinite Factor Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 965-969
-
- Article
-
- You have access
- Export citation
On the Irreducible Lattices of Orders
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 970-976
-
- Article
-
- You have access
- Export citation
Remarque Sur La Moyenne Arithmetique de Fonctions Univalentes Convexes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 977-981
-
- Article
-
- You have access
- Export citation
Mean Value and Limit Theorems for Generalized Matrix Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 982-991
-
- Article
-
- You have access
- Export citation
Minimal Decompositions of Complete Graphs into Subgraphs with Embeddability Properties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 992-1000
-
- Article
-
- You have access
- Export citation
A Note about Locally Spherical Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1003
-
- Article
-
- You have access
- Export citation
Archimedean Closures in Lattice-Ordered Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1004-1012
-
- Article
-
- You have access
- Export citation
The Asymptotic behaviour Of μ(z, β, α)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1013-1023
-
- Article
-
- You have access
- Export citation
Correction
On Some Methods of Construction of B.I.B. Designs: Corrigendum
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 1024
-
- Article
-
- You have access
- Export citation
Research Article
Finite Linear Groups of Prime Degree
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1025-1041
-
- Article
-
- You have access
- Export citation
Finite Linear Groups of Degree Seven. I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1042-1053
-
- Article
-
- You have access
- Export citation
Projective Ideals of Finite Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1057-1061
-
- Article
-
- You have access
- Export citation
On Simply Transitive Primitive Permutation Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1062-1068
-
- Article
-
- You have access
- Export citation
Extremal Point and Edge Sets in n-Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1069-1075
-
- Article
-
- You have access
- Export citation
Transformations Affines Agissant Sur Un Ensemble Compact Convexe
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1076-1082
-
- Article
-
- You have access
- Export citation
A Note on the Construction of Projective Planes from Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1083-1085
-
- Article
-
- You have access
- Export citation
 . We assume furthermore that
. We assume furthermore that 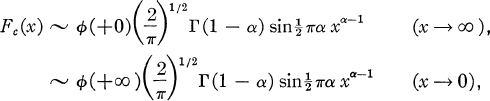
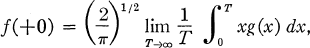
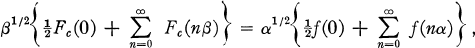
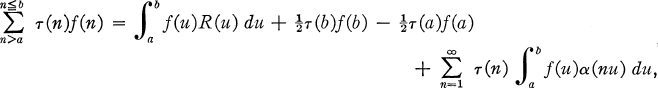
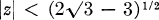 sur un domaine convexe et l'estimation est précise.
sur un domaine convexe et l'estimation est précise.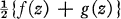 des deux fonctions
des deux fonctions 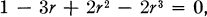
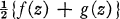 applique |
applique |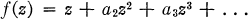
 of complex numbers. Denote by
of complex numbers. Denote by 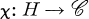 a character of degree 1 on
a character of degree 1 on 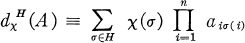
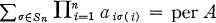 the permanent function. If the sequences ω = (ω
the permanent function. If the sequences ω = (ω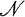 of
of 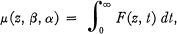
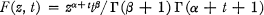
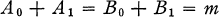
 of substitutions
of substitutions 