We study bubble break-up in homogeneous and isotropic turbulence by direct numerical simulations of the two-phase incompressible Navier–Stokes equations. We create the turbulence by forcing in physical space and introduce the bubble once a statistically stationary state is reached. We perform a large ensemble of simulations to investigate the effect of the Weber number (the ratio of turbulent and surface tension forces) on bubble break-up dynamics and statistics, including the child bubble size distribution, and discuss the numerical requirements to obtain results independent of grid size. We characterize the critical Weber number below which no break-up occurs and the associated Hinze scale $d_h$. At Weber number close to stable conditions (initial bubble sizes $d_0\approx d_h$), we observe binary and tertiary break-ups, leading to bubbles mostly between $0.5d_h$ and $d_h$, a signature of a production process local in scale. For large Weber numbers ($d_0> 3d_h$), we observe the creation of a wide range of bubble radii, with numerous child bubbles between $0.1d_h$ and $0.3d_h$, an order of magnitude smaller than the parent bubble. The separation of scales between the parent and child bubble is a signature of a production process non-local in scale. The formation mechanism of these sub-Hinze scale bubbles relates to rapid large deformation and successive break-ups: the first break-up in a sequence leaves highly deformed bubbles which will break again, without recovering a spherical shape and creating an array of much smaller bubbles. We discuss the application of this scenario to the production of sub-Hinze bubbles under breaking waves.

Experiments are presented on the Richtmyer–Meshkov instability (RMI) with a three-dimensional, multi-mode initial perturbation. The experiments use a vertical shock tube, where a stably stratified interface is formed between air and sulphur hexafluoride (SF$_6$) via counterflow. A perturbation is imposed at the interface by vertical oscillation of the gas column, forming Faraday waves. The interface is accelerated by a Mach 1.17 (in air) shock wave, and the development of the mixing region between the gases is investigated using particle image velocimetry. Following shock acceleration, a reflected shock wave from the bottom of the shock tube interacts with the mixing layer a second time (reshock). The experiment is initialized with both high and low amplitude perturbations to examine the effect of the perturbation amplitude on measured quantities. The instability growth exponent ($\theta$) is determined from the kinetic energy field using the width of the mixing layer and the decay of kinetic energy, which are found to be in agreement when the flow is most strongly excited. A growth exponent of $\theta \approx 0.5$ is found for all cases except the high-amplitude reshocked regime (where $\theta \approx 0.33$). High-amplitude experiments exhibit the transitional outer Reynolds number $(Re \equiv {h \dot {h}}/{\nu } > 10^4)$ required for mixing transition following the incident shock, and both experiments are elevated well above this threshold following reshock. However, neither set of experiments meet the more stringent requirements proposed by Zhou et al. (Phys. Rev.E, vol. 67, issue 5, 2003) which include the time dependent aspect of the RMI, an observation which is also made when examining the spectra.

We stabilize the flow past a cluster of three rotating cylinders – the fluidic pinball – with automated gradient-enriched machine learning algorithms. The control laws command the rotation speed of each cylinder in an open- and closed-loop manner. These laws are optimized with respect to the average distance from the target steady solution in three successively richer search spaces. First, stabilization is pursued with steady symmetric forcing. Second, we allow for asymmetric steady forcing. And third, we determine an optimal feedback controller employing nine velocity probes downstream. As expected, the control performance increases with every generalization of the search space. Surprisingly, both open- and closed-loop optimal controllers include an asymmetric forcing, which surpasses symmetric forcing. Intriguingly, the best performance is achieved by a combination of phasor control and asymmetric steady forcing. We hypothesize that asymmetric forcing is typical for pitchfork bifurcated dynamics of nominally symmetric configurations. Key enablers are automated machine learning algorithms augmented with gradient search: explorative gradient method for the open-loop parameter optimization and a gradient-enriched machine learning control (gMLC) for the feedback optimization. Gradient-enriched machine learning control learns the control law significantly faster thanpreviously employed genetic programming control. The gMLC source code is freely available online.

The transient dynamics of accelerating turbulent pipe flow has been examined using direct numerical simulation (DNS) data sets with a high spatiotemporal resolution, starting from low and moderate Reynolds numbers. The time-dependent evolution of the mean flow dynamics reveals that internal flows, during and after a rapid increase in the flow rate, experience four unambiguous transient stages: inertial, pre-transition, transition and core relaxation before they reach their final steady-state. The first stage is characterised by a rapid and substantial increment in the viscous forces within the viscous sublayer, together with the frozen behaviour of the existing turbulent eddies. The pre-transitional stage reveals a weak response of the turbulent inertia within the near-wall region, together with a rapid reduction in the viscous forces. At the third stage, termed transition, balanced growth in the magnitude of both the turbulent and the viscous forces within $y^{+0} \lesssim 50$ is observed. The final stage, referred to as core relaxation, shows a quasi-steady behaviour at $y^{+0} < 50$ and reveals the slow propagation of turbulence from the near-wall region into the wake region. A decomposition of the skin friction coefficient ($C_f$), using an FIK identity suitable for unsteady pipe flow, shows a progressive increment in the turbulent contribution during the core-relaxation period. Simultaneously, the unsteady contribution decreases proportionally, maintaining a plateau in $C_f$. The principal mechanism responsible for this slow regeneration in the wake is a temporal turbulence stratification at the inner region of the flow, together with a quiescent core, which maintains geometric coherence across extensive periods.

When an object is accelerated in a fluid, a primary vortex is formed through the roll-up of a shear layer. This primary vortex does not grow indefinitely and will reach a limiting size and strength. Additional vorticity beyond the critical limit will end up in a trailing shear layer and accumulate into secondary vortices. The secondary vortices are typically considerably smaller than the primary vortex. In this paper, we focus on the formation, shedding and trajectory of secondary vortices generated by a rotating rectangular plate in a quiescent fluid using time-resolved particle image velocimetry. The Reynolds number $\textit {Re}$ based on the maximum rotational velocity of the plate and the distance between the centre of rotation and the tip of the plate is varied from 840 to 11 150. At low $\textit {Re}$, the shear layer is a continuous uninterrupted layer of vorticity that rolls up into a single coherent primary vortex. At $\textit {Re} = 1955$, the shear layer becomes unstable and secondary vortices emerge and subsequently move away from the tip of the plate. For $\textit {Re} > 4000$, secondary vortices are discretely released from the plate tip and are not generated from the stretching of an unstable shear layer. First, we demonstrate that the roll-up of the shear layer, the trajectory of the primary vortex and the path of secondary vortices can be predicted by a modified Kaden spiral for the entire $\textit {Re}$ range considered. Second, the timing of the secondary vortex shedding is analysed using the swirling strength criterion. The separation time of each secondary vortex is identified as a local maximum in the temporal evolution of the average swirling strength close to the plate tip. The time interval between the release of successive secondary vortices is not constant during the rotation but increases the more vortices have been shed. The shedding time interval also increases with decreasing Reynolds number. The increased time interval under both conditions is due to a reduced circulation feeding rate.

We study the flow of water waves over bathymetry that varies periodically along one direction. We derive a linearized, homogenized model and show that the periodic bathymetry induces an effective dispersion, distinct from the dispersion inherently present in water waves. We relate this dispersion to the well-known effective dispersion introduced by changes in the bathymetry in non-rectangular channels. Numerical simulations using the (non-dispersive) shallow water equations reveal that a balance between this effective dispersion and nonlinearity can create solitary waves. We derive a Korteweg–de Vries-type equation that approximates the behaviour of these waves in the weakly nonlinear regime. We show that, depending on geometry, dispersion due to bathymetry can be much stronger than traditional water wave dispersion and can prevent wave breaking in strongly nonlinear regimes. Computational experiments using depth-averaged water wave models confirm the analysis and suggest that experimental observation of these solitary waves is possible.

Air bubbles at the surface of water end their life in a particular way: when bursting, they may eject drops of liquid in the surrounding environment. Many uncertainties remain regarding collective effects of bubbles at the water–air interface, despite extensive efforts to describe the bursting mechanisms, motivated by their critical importance in mass transfers between the ocean and the atmosphere in the production of sea spray aerosols. We investigate the effect of surfactant on the collective dynamics and statistics of air bubbles evolving freely at the surface of water, through an experimental set-up controlling the bulk distribution of bubbles with nearly monodisperse millimetric air bubbles. We observe that for low contamination, bubble coalescence is inevitable and leads to a broad surface size distribution. For higher surfactant concentrations, coalescence at the surface is prevented and bubble lifetime is increased, leading to the formation of rafts with a surface size distribution identical to the bulk distribution. This shows that surface contamination has a first-order influence on the transfer function from bulk size distribution to surface size distribution, an intermediate step which needs to be considered when developing sea spray source function as droplet production by bubble bursting depends on the bubble size. We measure the bursting and merging rates of bubbles as a function of contamination through a complementary freely decaying raft experiment. We propose a cellular automaton model that includes the minimal ingredients to reproduce the experimental results in the statistically stationary configuration: production, coalescence and bursting after a finite lifetime.

We investigate the behaviour of microscopic heavy particles settling in homogeneous air turbulence. The regimes are relevant to the airborne transport of dust and droplets: the Taylor-microscale Reynolds number is $Re_\lambda = 289\text {--}462$, the Kolmogorov-scale Stokes number is $St = 1.2\text {--}13$ and the Kolmogorov acceleration is comparable to the gravitational acceleration (i.e. the Froude number $Fr = O(1)$). We use high-speed laser imaging to track the particles and simultaneously characterize the air velocity field, resolving all relevant spatio-temporal scales. The role of the flow sampled by the particles is spotlighted. In the present range of parameters, the particle settling velocity is enhanced proportionally to the velocity scale of the turbulence. Both gravity and inertia reduce the velocity fluctuations of the particles compared to the fluid; while they have competing effect on the particle acceleration, through the crossing trajectories and inertial filtering mechanisms, respectively. The preferential sampling of high-strain/low-vorticity regions is measurable, but its impact on the global statistics is moderate. The inertial particles have large relative velocity at small separations, which increases their pair dispersion; however, gravity offsets this effect by causing them to experience fluid velocities that decorrelate faster in time compared to tracers. Based on the observations, we derive an analytical model to predict the particle velocity and acceleration variances for arbitrary $St$, $Fr$ and $Re_\lambda$. This agrees well with the present observations and previous simulations and captures the respective effects of inertia and gravity, both of which play crucial roles in the transport.

Baroclinic critical levels arise as singularities in the inviscid linear theory of waves propagating through a stratified, horizontally directed and sheared flow. For a steady wave forcing, disturbances grow secularly over the critical layers surrounding these levels, generating a jet-like defect in the mean flow. We use a matched asymptotic expansion to furnish a reduced model of the nonlinear dynamics of such defects. By solving the linear initial-value problem for small perturbations to the defect, we establish that secondary instabilities appear at later times. Because the defect is time dependent, conventional normal-mode analysis is quantitatively inaccurate, but does successfully predict the occurrence of the secondary instability. The instability has a singular character in that disturbances with the shortest horizontal wavelength grow most vigorously at late times, unless dissipation is included. The instability can be suppressed by weak viscosity; by itself, thermal dissipation delays, but does not arrest instability. Numerical computations with the dissipative reduced model demonstrate that the secondary instability saturates as the defect rolls up into a coherent vortical structure. This structure excites a new wave propagating at a different phase speed, thereby forcing a new set of baroclinic critical levels. The implications for self-replication are discussed.

In confined stratified basins, wind forcing is an important mechanism responsible for the onset and generation of internal waves and seiches. Previous observations have also found that gravity currents in stratified environments can also initiate internal waves. We conducted a series of laboratory experiments to investigate the generation of internal motions due to such dense gravity currents on an incline entering a two-layer stratification, focusing in particular on the interaction between the onset of internal motions and topography and diapycnal mixing due to breaking internal waves. The baroclinic response of the ambient stratification to the gravity current is found to be analogous to a system forced by a surface wind stress, and the response as characterized by a Wedderburn-like number was found to be linearly proportional to the initial gravity current Richardson number. The generated internal motions are characterized as having a low-frequency internal surge and higher-frequency progressive internal waves. The overall mixing efficiency of the breaking internal wave was calculated and found to be low compared with similar previous studies.

Here, we present experimental results of water and ethanol drops of radii 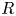$R$, density $\rho$ and interfacial tension coefficient 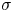$\sigma$, impacting with a velocity $V$ over different types of sandpapers containing particles of characteristic diameter $\varepsilon$ embedded in their surfaces. It is shown that the transition from spreading to splashing at normal atmospheric conditions can be classified depending on the value of the parameter $\varepsilon /H_t\simeq We_\varepsilon =We(\varepsilon /R)$, with $We=\rho V^2 R/\sigma$ the Weber number and $H_t$ indicating the initial thickness of the thin film – the lamella – which is ejected along the substrate once the drop touches the solid. When $We_\varepsilon \lesssim 1$ and the liquid wets the substrate, the critical value of the Weber number above which the drop splashes, 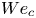$We_c$, can be predicted using the results in Gordillo & Riboux (J. Fluid Mech., vol. 871, 2019, R3) once the angle the advancing rim forms with the substrate, $\alpha$, is expressed as a decreasing function of the static advancing contact angle. The calculated values of 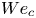$We_c$ for the case of water drops impacting over rough substrates are smaller than the corresponding ones for smooth substrates, in agreement with experimental observations. Moreover, if the liquid does not wet the substrate, it is also shown that the splash velocity can be predicted using the theory for superhydrophobic substrates in Quintero, Riboux & Gordillo (J. Fluid Mech., vol. 870, 2019, 175–188). For those cases in which $We_\varepsilon \gtrsim 1$ and the liquid wets the substrate, we demonstrate that the critical Weber number for splashing decreases with $\varepsilon$ as $We_c\propto (R\cos \theta _0 /\varepsilon )^{3/5}$, with $\theta _0$ the value of the Young contact angle.

Granular column collapse involves complicated granular flow bridging initial and final solid-like states, with intermediate multi-regime spatial and temporal flow patterns and transitions, which include large free-surface variation. In this study, a non-local mesh-free numerical method is proposed to model these flows and capture the entire process from flowing to arresting. Free surface evolution is tracked by the mesh-free method while the non-local theory of peridynamics is used to capture the arresting for the flow. 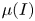The constitutive relation to calculate the effective viscosity and stress is based on the μ(I) rheology. The non-local mesh-free method is validated to simulate a granular column collapse in which effects from the peridynamic horizon and particle distance are both examined. Non-local modelling is then used to simulate more types of granular column collapses, by comparison with other numerical results and experimental observations in terms of the free surface and velocity variations in both the fluid-like and solid-like states. The collision between two adjacent collapsing granular columns is also simulated, and the interface variations between material from each collapsing column are compared with experimental observations. The non-local modelling is shown to reflect the internal flow characteristics in the granular flow. Throughout these simulations, the non-local mesh-free method is able to calculate the free surface, velocity and interface variation in the granular flows.

We conduct an asymptotic analysis to derive a macrotransport equation for the long-time transport of a chemotactic/diffusiophoretic colloidal species in a uniform circular tube under a steady, laminar, pressure-driven flow and transient solute gradient. The solute gradient drives a ‘log-sensing’ advective flux of the colloidal species, which competes with Taylor dispersion due to the hydrodynamic flow. We demonstrate excellent agreement between the macrotransport equation and direct numerical solution of the full advection–diffusion equation for the colloidal species transport. In addition to its accuracy, the macrotransport equation requires $O(10^3)$ times less computational runtime than direct numerical solution of the advection–diffusion equation. Via scaling arguments, we identify three regimes of the colloidal species macrotransport, which span from chemotactic/diffusiophoretic-dominated macrotransport to the familiar Taylor dispersion regime, where macrotransport is dominated by the hydrodynamic flow. Finally, we discuss generalization of the macrotransport equation to channels of arbitrary (but constant) cross-section and to incorporate more sophisticated models of chemotactic fluxes. The macrotransport framework developed here will broaden the scope of designing chemotactic/diffusiophoretic transport systems by elucidating the interplay of macrotransport due to chemotaxis/diffusiophoresis and hydrodynamic flow.

It has been suggested that a cellularly unstable laminar flame, which is freely propagating in unbounded space, can accelerate and evolve into a turbulent flame with the neighbouring flow exhibiting the basic characteristics of turbulence. Famously known as self-turbulization, this conceptual transition in the flow regime, which arises from local interactions between the propagating wrinkled flamefront and the flow, is critical in extreme events such as the deflagration-to-detonation transition (DDT) leading to supernova explosions. Recognizing that such a transition in the flow regime has not been conclusively demonstrated through experiments, in this work, we present experimental measurements of flow characteristics of flame-generated ‘turbulence’ for expanding cellular laminar flames. The energy spectra of such ‘turbulence’ at different stages of cellular instability are analysed. A subsequent scaling analysis points out that the observed energy spectra are driven by the fractal topology of the cellularly unstable flamefront.

We present a theoretical and experimental study of the dynamics of two-layer viscous fluid flows on inclined surfaces, motivated by natural and industrial phenomena involving the interactions between two fluid layers. A general model describing the evolution of two fluids on an inclined substrate is developed and explored to reveal a rich variety of flow regimes for different modes of release. The asymptotic reduction of this problem due to the dominance of the along-slope component of gravity is shown to yield considerable analytical inroads compared with previous studies of multi-layer flow configurations, which have focused exclusively on the case of horizontal beds. For the canonical example in which two fluids are introduced at a constant flux, the flow forms two regions: an upstream region containing both fluids, and a downstream region comprised purely of the lighter fluid, with a sharp intervening jump in thicknesses between the two. By constructing similarity solutions, we establish a full regime diagram of the possible configurations over all asymptotic limits of the viscosity, flux and density ratios. For the release of two fixed volumes of fluid, the layers separate completely into two disjoint but connected regions, contrasting in essential structure from the constant flux case. Even a small volume of the heavier fluid is able to significantly accelerate the propagation of the lighter fluid in front of it. Excellent agreement is found between our theoretical predictions and the results of a series of laboratory experiments.

We carry out direct numerical simulations of turbulent flow over riblets, streamwise- aligned grooves that are designed to reduce drag by modifying the near-wall flow. Twenty riblet geometries and sizes are considered, namely symmetric triangular with tip angle $30^\circ$, $60^\circ$ and $90^\circ$, asymmetric triangular, blade and trapezoidal. To save on computational cost, simulations are performed using the minimal-channel flow configuration. With this unprecedented breadth of high-fidelity flow data near the wall, we are able to obtain more general insights into the flow physics of riblets. As observed by García-Mayoral & Jiménez (J. Fluid Mech., vol. 678, 2011, pp. 317–347), we confirm that the drag-change curves of all the present groove geometries better collapse when reported with the viscous-scaled square root of the groove area $\ell _g^+$, rather than the riblet spacing $s^+$. Using a two-dimensional generalization of the Fukagata–Iwamoto–Kasagi identity in difference form we isolate the different drag-change contributions. We show that the drag increase associated with dispersive stresses carried by secondary flows can be as important as the one associated with the turbulent stresses and the pre-eminence of dispersive stresses can be estimated by the groove width at the riblet mean height.

We consider the downstream development of small amplitude unsteady disturbances on a (Blasius) boundary layer. Two-dimensional disturbances have received much attention in the past, but herein lies an interesting conundrum, namely that two completely disparate families exist. The first, originally found by Lam & Rott and Ackerberg & Phillips, is located deep inside the boundary layer, and decays exponentially downstream with an increasingly short wavelength. The other family, originally found by Brown & Stewartson, is centred at the outer edge of the boundary layer, and exhibits slower decay than the former family. In this paper, we consider three-dimensional disturbances. Initially we mount a downstream ‘marching’ approach based on the ‘boundary-region’ equations, wherein spanwise scales are (notionally) comparable to the boundary-layer thickness. These calculations strongly suggest that disturbance growth is possible downstream, in contrast to two-dimensional disturbances that (on the streamwise length scales considered) all decay. We then mount a (heuristic) numerical investigation, performing a locally parallel eigenmode search at increasing downstream locations. This indicates that, for two-dimensional disturbances, with increasingly downstream locations, progressively more eigenmodes evolve, that are clearly linked to the Lam & Rott and Ackerberg & Phillips family, being spawned from what appears to be the Brown & Stewartson variety. These results also clearly indicate three-dimensionality can have a profound effect on the two-dimensional modes, including the potential for downstream growth. This provides an explanation for the downstream growth witnessed in the downstream-developing calculations, and is then conclusively confirmed by (mathematically rigorous) asymptotic analyses, valid far downstream.

We revisit two-dimensional channel flow with fixed volume flux for Reynolds numbers $Re\in [7000,72\,000]$ via direct numerical simulations and uncover a region of multistability of turbulent states. New asymmetric states (based on comparing the time-averaged mean shear on each of the channel walls) exist for at least $32\,000\,h/U$ when $Re \in [21\,000, 42\,000]$ alongside the known symmetric solution ($2h$ is the channel height and $U$ is the mean flow rate). Both the symmetric and asymmetric states resemble a travelling wave even at $Re$ an order of magnitude above the primary bifurcation at $Re=5772$ with the asymmetric state showing heightened turbulent behaviour near one of the channel walls. These asymmetric states display up to $22\,\%$ reduction in pressure gradient compared with their symmetric counterparts. The saddle state between the two apparent attractors is shown to be the travelling wave solution which originates from the primary bifurcation. By $Re=43\,000$, the symmetric solution has become unstable leaving only the asymmetric state and its reflected counterpart as attractors until at least $Re=46\,875$. At $Re=60\,000$, the pair of asymmetric states become connected so that the ‘turbulent’ wall switches apparently randomly and infrequently. In this way, the symmetry of the flow is then restored but only after averaging over extremely long times ($\gg 10^5 h/U$).

The thermal conductivity of a molecular gas consists of the translational and internal parts. Although in continuum flows the total thermal conductivity itself is adequate to describe the heat transfer, in rarefied gas flows they need to be modelled separately, according to the relaxation rates of translational and internal heat fluxes in an homogeneous system. This paper is dedicated to quantifying how these relaxation rates affect rarefied gas dynamics. The kinetic model of Wu et al. (J. Fluid Mech., vol. 763, 2015, pp. 24–50) is adapted to recover the relaxation of heat fluxes, which is validated by the direct simulation Monte Carlo method. Then the model of Wu et al., which has the freedom to adjust the relaxation rates, is used to investigate the rate effects of thermal relaxation in problems such as the normal shock wave, creep flow driven by Maxwell's demon and thermal transpiration. It is found that the relaxation rates of heat flux affect rarefied gas flows significantly, even when the total thermal conductivity is fixed.