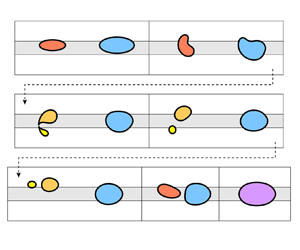
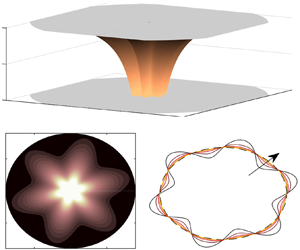
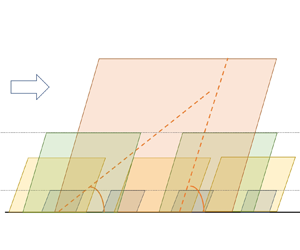
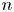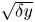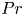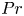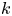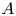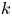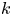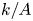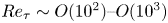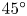Graphical abstract from Brandner, P., Venning, J. & Pearce, B. 2022 Nucleation effects on cavitation about a sphere. J. Fluid Mech. 946, A1. doi:10.1017/jfm.2022.511.
JFM Papers
Influence of jet spacing in spanwise-inclined jet injection in supersonic crossflow
-
- Published online by Cambridge University Press:
- 11 August 2022, A39
-
- Article
- Export citation
The interaction of multiple bubbles in a Hele-Shaw channel
-
- Published online by Cambridge University Press:
- 11 August 2022, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
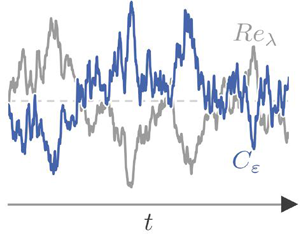
Scalings of turbulence dissipation in space and time for turbulent channel flow
-
- Published online by Cambridge University Press:
- 11 August 2022, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling the transport equation of the scalar structure function
-
- Published online by Cambridge University Press:
- 11 August 2022, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of an inertially collapsing gas bubble between two parallel, rigid walls
-
- Published online by Cambridge University Press:
- 11 August 2022, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Suppression of flow reversals via manipulating corner rolls in plane Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 11 August 2022, A44
-
- Article
- Export citation
Shear-induced motion of a bead on regular substrates at small particle Reynolds numbers
-
- Published online by Cambridge University Press:
- 11 August 2022, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of a fluid-infused patch from droplet drainage into a thin porous layer
-
- Published online by Cambridge University Press:
- 17 August 2022, A46
-
- Article
- Export citation
Baroclinic tidal conversion: note on a paper of L.R.M. Maas
-
- Published online by Cambridge University Press:
- 12 August 2022, A47
-
- Article
- Export citation
Buoyancy segregation suppresses viscous fingering in horizontal displacements in a porous layer
-
- Published online by Cambridge University Press:
- 12 August 2022, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Streamwise inclination angle of wall-attached eddies in turbulent channel flows
-
- Published online by Cambridge University Press:
- 12 August 2022, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 946 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 August 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation