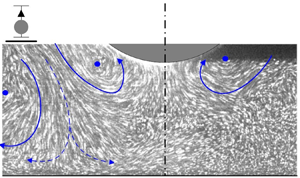
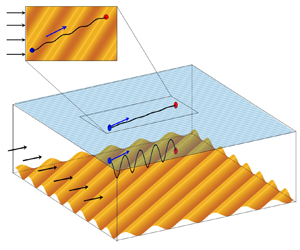
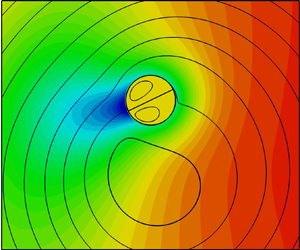
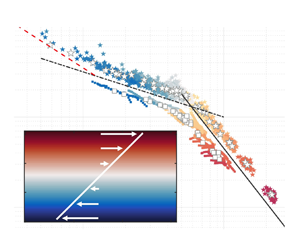
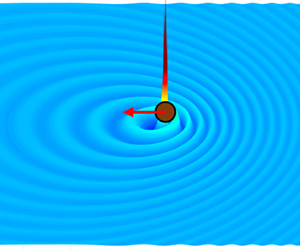
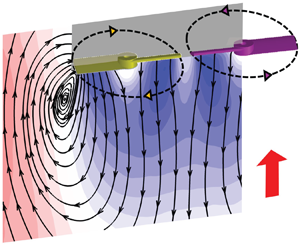
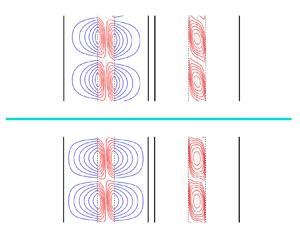
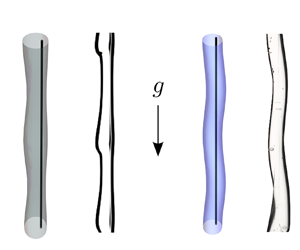
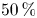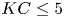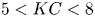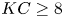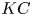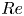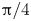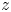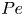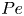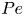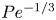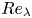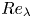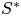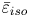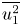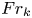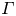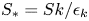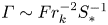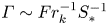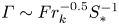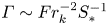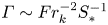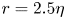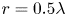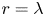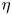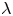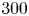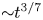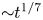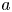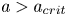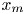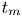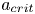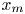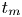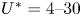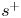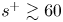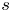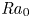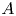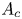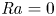Graphical abstract from Endrikat, S., Newton, R., Modesti, D., García-Mayoral, R., Hutchins, N. & Chung, D. 2022 Reorganisation of turbulence by large and spanwise-varying riblets. J. Fluid Mech. 952, A27. doi:10.1017/jfm.2022.897.
Contents
JFM Papers
Observations of pumping and vortex dynamics due to a cylinder oscillating normal to a plane wall
-
- Published online by Cambridge University Press:
- 24 November 2022, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new Lagrangian drift mechanism due to current–bathymetry interactions: applications in coastal cross-shelf transport
-
- Published online by Cambridge University Press:
- 24 November 2022, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of a self-propelled compound droplet
-
- Published online by Cambridge University Press:
- 24 November 2022, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approach towards local isotropy in statistically stationary turbulent shear flows
-
- Published online by Cambridge University Press:
- 24 November 2022, A17
-
- Article
- Export citation
Revised mixing coefficient scaling for sheared stably stratified turbulence
-
- Published online by Cambridge University Press:
- 24 November 2022, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Active Stokesian dynamics
-
- Published online by Cambridge University Press:
- 28 November 2022, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the simultaneous cascades of energy, helicity, and enstrophy in incompressible homogeneous turbulence
-
- Published online by Cambridge University Press:
- 24 November 2022, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dissimilar turbulent heat transfer enhancement by Kelvin–Helmholtz rollers over high-aspect-ratio longitudinal ribs
-
- Published online by Cambridge University Press:
- 24 November 2022, A21
-
- Article
- Export citation
Self-radiation force on a moving monopolar source
-
- Published online by Cambridge University Press:
- 28 November 2022, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Axisymmetric gravity currents in anisotropic porous media
-
- Published online by Cambridge University Press:
- 24 November 2022, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
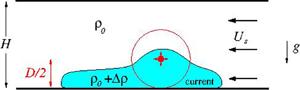
On simple models for gravity currents from moving sources
-
- Published online by Cambridge University Press:
- 24 November 2022, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved modelling of interfacial terms in the second-moment closure for particle-laden flows based on interface-resolved simulation data
-
- Published online by Cambridge University Press:
- 24 November 2022, A25
-
- Article
- Export citation
Vortex-induced vibration of a two degree-of-freedom flexibly mounted circular cylinder in the crossflow direction
-
- Published online by Cambridge University Press:
- 28 November 2022, A26
-
- Article
- Export citation
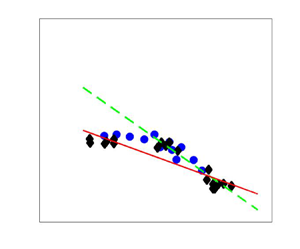
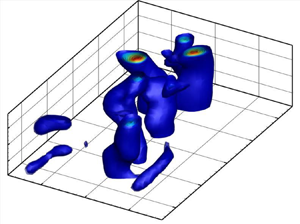
Reorganisation of turbulence by large and spanwise-varying riblets
-
- Published online by Cambridge University Press:
- 28 November 2022, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steady and oscillatory flows generated by Eckart streaming in the two-dimensional Rayleigh–Bénard configuration
-
- Published online by Cambridge University Press:
- 28 November 2022, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic cavitation reduction in semidilute turbulent polymer solution flows
-
- Published online by Cambridge University Press:
- 28 November 2022, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free surface in two-dimensional potential flow: singularities, invariants and virtual fluid
-
- Published online by Cambridge University Press:
- 28 November 2022, A30
-
- Article
- Export citation
Effects of rotor–rotor interaction on the wake characteristics of twin rotors in axial descent
-
- Published online by Cambridge University Press:
- 28 November 2022, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gill's problem in a sandwiched porous slab
-
- Published online by Cambridge University Press:
- 29 November 2022, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Whirling instability of an eccentric coated fibre
-
- Published online by Cambridge University Press:
- 29 November 2022, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation