 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
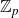 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
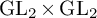 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
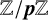 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
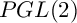 $PGL(2)$
EXTENSION
$PGL(2)$
EXTENSION
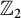 $\mathbb Z_2$
-extensions of real quadratic fields
$\mathbb Z_2$
-extensions of real quadratic fields