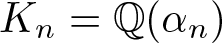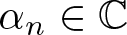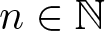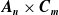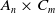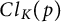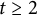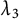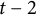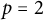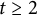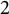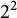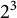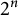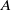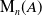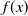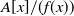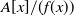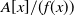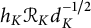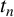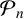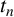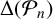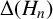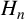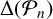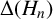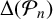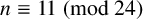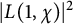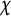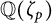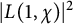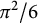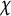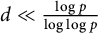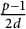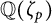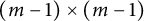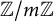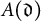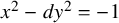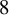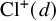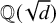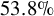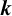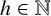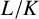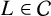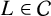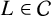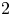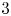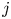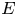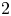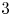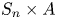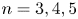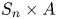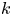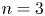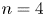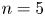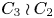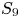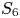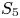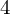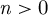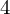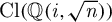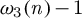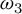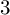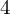90 results
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
-
- You have access
- HTML
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 460-467
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
NON-PÓLYA FIELDS WITH LARGE PÓLYA GROUPS ARISING FROM LEHMER QUINTICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 468-479
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
On
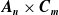 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite families of Artin–Schreier function fields with any prescribed class group rank
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1773-1794
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From the Ideal Theorem to the class number
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1368-1375
- Print publication:
- December 2023
-
- Article
- Export citation
ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN
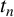 $t_n$ CLASS INVARIANTS
$t_n$ CLASS INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 264-275
- Print publication:
- October 2023
-
- Article
- Export citation
Mean square values of L-functions over subgroups for nonprimitive characters, Dedekind sums and bounds on relative class numbers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 1711-1743
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The shape of cyclic number fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 599-609
- Print publication:
- June 2023
-
- Article
- Export citation
The 8-rank of the narrow class group and the negative Pell equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 June 2022, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPLICATIONS OF CIRCULANT MATRICES TO DETERMINANTS INVOLVING
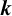 $\boldsymbol {k}$
TH POWER RESIDUES
$\boldsymbol {k}$
TH POWER RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 243-253
- Print publication:
- October 2022
-
- Article
- Export citation
ON STARK’S CLASS NUMBER CONJECTURE AND THE GENERALISED BRAUER–SIEGEL CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 288-300
- Print publication:
- October 2022
-
- Article
- Export citation
Large families of elliptic curves ordered by conductor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 1538-1583
- Print publication:
- July 2021
-
- Article
- Export citation
NOTE ON THE p-DIVISIBILITY OF CLASS NUMBERS OF AN INFINITE FAMILY OF IMAGINARY QUADRATIC FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 May 2021, pp. 352-357
- Print publication:
- May 2022
-
- Article
- Export citation
Malle's conjecture for
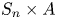 $S_n\times A$ for
$S_n\times A$ for 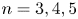 $n = 3,4,5$
$n = 3,4,5$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 83-121
- Print publication:
- January 2021
-
- Article
- Export citation
ON THE
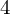 $4$
-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
$4$
-RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1543-1570
- Print publication:
- September 2022
-
- Article
- Export citation
CLASS NUMBERS OF CM ALGEBRAIC TORI, CM ABELIAN VARIETIES AND COMPONENTS OF UNITARY SHIMURA VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 74-99
- Print publication:
- March 2022
-
- Article
- Export citation
The Trace Form Over Cyclic Number Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 947-969
- Print publication:
- August 2021
-
- Article
- Export citation