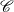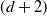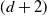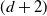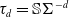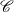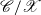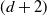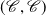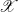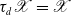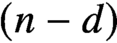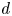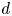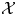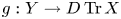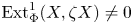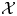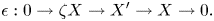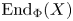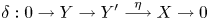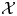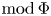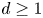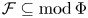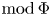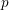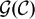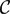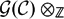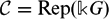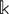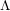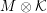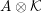29 results
Groups generated by two twists along spherical sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 137-161
- Print publication:
- January 2023
-
- Article
- Export citation
The generalized auslander–reiten duality on a module category
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 167-181
-
- Article
- Export citation
Higher-dimensional Auslander–Reiten theory on (d+2)-angulated categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 October 2021, pp. 527-547
- Print publication:
- September 2022
-
- Article
- Export citation
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
Higher preprojective algebras, Koszul algebras, and superpotentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 01 February 2021, pp. 2588-2627
- Print publication:
- December 2020
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
τ-Tilting finite cluster-tilted algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 950-955
-
- Article
- Export citation
d-Auslander–Reiten sequences in subcategories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 15 January 2020, pp. 342-373
-
- Article
- Export citation
ALGEBRAS OF GENERALIZED DIHEDRAL TYPE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 February 2019, pp. 181-236
- Print publication:
- December 2020
-
- Article
- Export citation
ON COMPONENTS OF STABLE AUSLANDER–REITEN QUIVERS THAT CONTAIN HELLER LATTICES: THE CASE OF TRUNCATED POLYNOMIAL RINGS – CORRIGENDUM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 14 January 2019, pp. 211-216
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
SIMPLE MODULES IN THE AUSLANDER–REITEN QUIVER OF PRINCIPAL BLOCKS WITH ABELIAN DEFECT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 05 February 2018, pp. 58-85
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
A CRITERION FOR THE JACOBSON SEMISIMPLICITY OF THE GREEN RING OF A FINITE TENSOR CATEGORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 25 September 2017, pp. 253-272
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
LATTICE STRUCTURE OF TORSION CLASSES FOR HEREDITARY ARTIN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 05 June 2017, pp. 89-100
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON COMPONENTS OF STABLE AUSLANDER–REITEN QUIVERS THAT CONTAIN HELLER LATTICES: THE CASE OF TRUNCATED POLYNOMIAL RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 72-113
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
DISTRIBUTIVE LATTICES OF TILTING MODULES AND SUPPORT τ-TILTING MODULES OVER PATH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 503-511
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
Generalized friezes and a modified Caldero–Chapoton map depending on a rigid object
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 101-124
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Quotient closed subcategories of quiver representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
- Print publication:
- March 2015
-
- Article
- Export citation
Algebras of acyclic cluster type: Tree type and type Ã
-
- Journal:
- Nagoya Mathematical Journal / Volume 211 / September 2013
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-50
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
ON CRYSTAL OPERATORS IN LUSZTIG'S PARAMETRIZATIONS AND STRING CONE DEFINING INEQUALITIES
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 177-200
- Print publication:
- January 2013
-
- Article
-
- You have access
- Export citation
Cluster structures for 2-Calabi–Yau categories and unipotent groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 1035-1079
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation