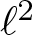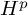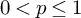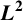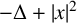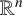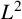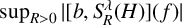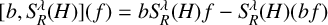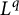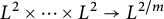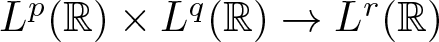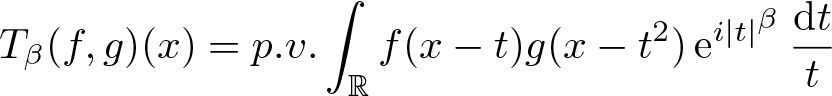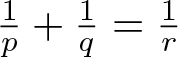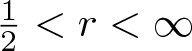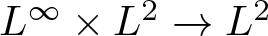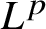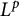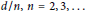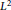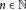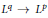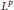30 results
SCHRÖDINGER PROPAGATOR ON WIENER AMALGAM SPACES IN THE FULL RANGE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 27 August 2024, pp. 953-969
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
-
- You have access
- HTML
- Export citation
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2217-2278
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
A WEIGHTED
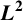 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
On pointwise a.e. convergence of multilinear operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1005-1032
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
The boundedness of the bilinear oscillatory integral along a parabola
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 54-88
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oscillating multipliers on symmetric and locally symmetric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 887-905
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal functions associated with families of homogeneous curves: Lp bounds for P ≤ 2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 398-412
-
- Article
- Export citation
Two boundedness criteria for a class of operators on Musielak–Orlicz Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 13-35
-
- Article
- Export citation
Convolution Powers of Salem Measures With Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-320
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
Sharp Localized Inequalities for Fourier Multipliers
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1358-1381
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Lp-Spectral Multipliers for some Elliptic Systems
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 October 2014, pp. 231-253
-
- Article
-
- You have access
- Export citation
Pointwise multipliers for Campanato spaces on Gauss measure spaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 214 / June 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 169-193
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Transference of Vector-valued Multipliers on Weighted Lp-spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 3 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 510-543
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
On Multilinear Fourier Multipliers of Limited Smoothness
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 299-330
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation
Representing Multipliers of the Fourier Algebra on Non-Commutative Lp Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 798-825
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
NECESSARY CONDITIONS FOR VECTOR-VALUED OPERATOR INEQUALITIES IN HARMONIC ANALYSIS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 93 / Issue 2 / September 2006
- Published online by Cambridge University Press:
- 07 August 2006, pp. 447-473
- Print publication:
- September 2006
-
- Article
- Export citation
On a Class of Singular Integral Operators With Rough Kernels
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 1 / 01 March 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
- Print publication:
- 01 March 2006
-
- Article
-
- You have access
- Export citation

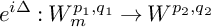
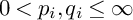 and
and