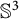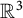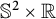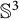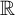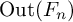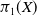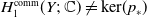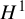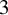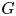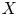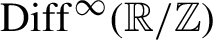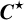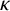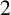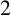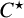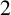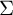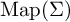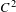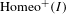31 results
Discrete group actions on 3-manifolds and embeddable Cayley complexes
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant covering type and the number of vertices in equivariant triangulations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2365-2403
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR GROWTH OF TRANSLATION LENGTHS OF RANDOM ISOMETRIES ON GROMOV HYPERBOLIC SPACES AND TEICHMÜLLER SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1751-1795
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subrepresentations in the homology of finite covers of graphs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 582-594
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper extensions of the 2-sphere’s conformal group present entropy and are 4-transitive
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 03 May 2023, pp. 1102-1122
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Equivariant Heegaard genus of reducible 3-manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 51-87
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Brill–Noether theory for elliptic operators and superrigidity of J-holomorphic maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 January 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flows, growth rates, and the veering polynomial
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 3026-3107
- Print publication:
- September 2023
-
- Article
- Export citation
Central limit theorems for counting measures in coarse negative curvature
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1980-2013
- Print publication:
- October 2022
-
- Article
- Export citation
Equivariant cobordisms between freely periodic knots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 450-457
- Print publication:
- June 2023
-
- Article
- Export citation
LIFTING HOMEOMORPHISMS AND FINITE ABELIAN BRANCHED COVERS OF THE 2-SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 02 June 2022, pp. 504-507
- Print publication:
- December 2022
-
- Article
- Export citation
Distortion in the group of circle homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 23 March 2022, pp. 1081-1086
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
THE K-THEORY OF THE
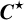 ${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 119-144
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG MAPPING CLASS GROUPS WITH HYPERBOLIC ACTIONS: CLASSIFICATION AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2173-2204
- Print publication:
- November 2022
-
- Article
- Export citation
A cancellation theorem for modules over integral group rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 27 November 2020, pp. 317-327
- Print publication:
- September 2021
-
- Article
- Export citation
Limits of geodesic push-forwards of horocycle invariant measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 23 October 2020, pp. 2782-2804
- Print publication:
- September 2021
-
- Article
- Export citation
CYCLIC BRANCHED COVERINGS OF BRIESKORN SPHERES BOUNDING ACYCLIC 4-MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 03 July 2020, pp. 400-413
- Print publication:
- May 2021
-
- Article
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation