25 results
Exact recovery of community detection in k-community Gaussian mixture models
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigid continuation paths II. structured polynomial systems
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional norms, condition numbers and numerical algorithms in algebraic geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IS CAUSAL REASONING HARDER THAN PROBABILISTIC REASONING?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 18 May 2022, pp. 106-131
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Yaglom limit for stochastic fluid models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 649-686
- Print publication:
- September 2021
-
- Article
- Export citation
Polynomial-time approximation algorithms for the antiferromagnetic Ising model on line graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 905-921
-
- Article
- Export citation
DECIDING SOME MALTSEV CONDITIONS IN FINITE IDEMPOTENT ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 June 2020, pp. 539-562
- Print publication:
- June 2020
-
- Article
- Export citation
Estimating parameters associated with monotone properties
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 616-632
-
- Article
- Export citation
Deciding the Existence of Minority Terms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 577-591
- Print publication:
- September 2020
-
- Article
- Export citation
ON FINDING SOLUTIONS TO EXPONENTIAL CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 388-391
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Dual-Pivot Quicksort: Optimality, Analysis and Zeros of Associated Lattice Paths
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 485-518
-
- Article
- Export citation
A GENERAL POSITION PROBLEM IN GRAPH THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 177-187
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
An Average Case NP-complete Graph Colouring Problem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 5 / September 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 808-828
-
- Article
- Export citation
An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low-level encoding of zero
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 255-266
-
- Article
-
- You have access
- Export citation
THE CONSTRAINT SATISFACTION PROBLEM AND UNIVERSALALGEBRA
-
- Journal:
- Bulletin of Symbolic Logic / Volume 21 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 15 September 2015, pp. 319-337
- Print publication:
- September 2015
-
- Article
- Export citation
Towards a Realistic Analysis of Some Popular Sorting Algorithms
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 11 December 2014, pp. 104-144
-
- Article
- Export citation
Pólya Urns Via the Contraction Method
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 1148-1186
-
- Article
- Export citation
On the use of expansion series for stream ciphers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
A Subalgebra Intersection Property for Congruence Distributive Varieties
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 2 / 01 April 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 451-464
- Print publication:
- 01 April 2009
-
- Article
-
- You have access
- Export citation
A Stochastic Maximin Fixed-Point Equation Related to Game Tree Evaluation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 586-606
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation



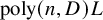
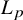
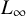
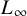
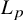

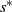
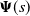
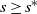
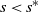
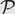

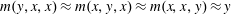
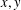
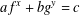
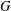
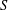
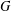
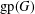

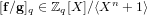
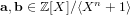
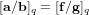
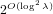
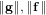
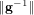


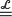 ξ max
ξ max