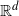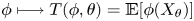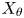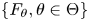Refine search
Actions for selected content:
194 results
The distribution of the minimum observation until a stopping time, with an application to the minimal spacing in a Renewal process
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-20
-
- Article
- Export citation
Optimal stopping with variable attention
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Langevin Equation and Fokker–Planck Equation
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 176-204
-
- Chapter
- Export citation
The Dependent Poisson Race Model and Modeling Dependence in Conjoint Choice Experiments
-
- Journal:
- Psychometrika / Volume 73 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 01 January 2025, pp. 261-288
-
- Article
- Export citation
Inferring species extinction from sighting data
-
- Journal:
- Cambridge Prisms: Extinction / Volume 2 / 2024
- Published online by Cambridge University Press:
- 25 November 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of concurrency on epidemic spreading in Markovian temporal networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 430-461
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the combined imperfect repair process
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 341-354
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The direct-connectedness function in the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 August 2022, pp. 179-222
- Print publication:
- March 2023
-
- Article
- Export citation
Nash equilibrium structure of Cox process Hotelling games
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 570-598
- Print publication:
- June 2022
-
- Article
- Export citation
Intersections of random sets
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 131-151
- Print publication:
- March 2022
-
- Article
- Export citation
11 - Time- and Space-Variant Reliability Analysis
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 357-404
-
- Chapter
- Export citation
Asymptotic behavior of the weak approximation to a class of Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 693-707
- Print publication:
- September 2021
-
- Article
- Export citation
1 - Counting Processes
- from Part I - Point Processes
-
- Book:
- Point Processes and Jump Diffusions
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 3-7
-
- Chapter
- Export citation
3 - More on Poisson Processes
- from Part I - Point Processes
-
- Book:
- Point Processes and Jump Diffusions
- Published online:
- 27 May 2021
- Print publication:
- 17 June 2021, pp 30-35
-
- Chapter
- Export citation
Ergodic control of diffusions with random intervention times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 1-21
- Print publication:
- March 2021
-
- Article
- Export citation
Almost sure central limit theorems in stochastic geometry
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 24 September 2020, pp. 705-734
- Print publication:
- September 2020
-
- Article
- Export citation
PRESERVATION OF LOG-CONCAVITY AND LOG-CONVEXITY UNDER OPERATORS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 35 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 14 February 2020, pp. 451-464
-
- Article
- Export citation
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Determination of Boolean models by densities of mixed volumes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 116-135
- Print publication:
- March 2019
-
- Article
- Export citation