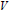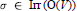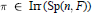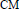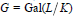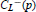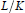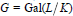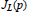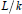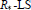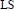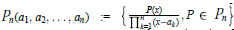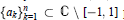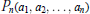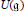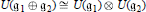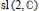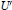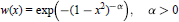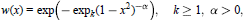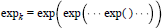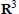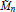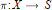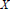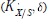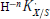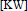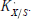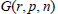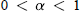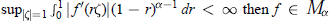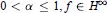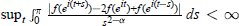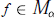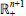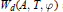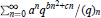Contents
Research Article
Tempered Representations and the Theta Correspondence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1105-1118
-
- Article
-
- You have access
- Export citation
On Critical Level Sets of Some two Degrees of Freedom Integrable Hamiltonian Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-151
-
- Article
-
- You have access
- Export citation
Primes in Short Segments of Arithmetic Progressions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 563-580
-
- Article
-
- You have access
- Export citation
Integral Representation of p -Class Groups In ℤp -Extensions and the Jacobian Variety
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1253-1272
-
- Article
-
- You have access
- Export citation
Lusternik-Schnirelmann Category and Algebraic R-Local Homotopy Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-862
-
- Article
-
- You have access
- Export citation
Inequalities for Rational Functions With Prescribed Poles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 152-166
-
- Article
-
- You have access
- Export citation
Some Norms on Universal Enveloping Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 356-377
-
- Article
-
- You have access
- Export citation
Mean Convergence of Lagrange Interpolation for Exponential weights on [-1, 1]
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1273-1297
-
- Article
-
- You have access
- Export citation
The Homology of Singular Polygon Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 581-594
-
- Article
-
- You have access
- Export citation
Smooth Formal Embeddings and the Residue Complex
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 863-896
-
- Article
-
- You have access
- Export citation
Equivariant Polynomial Automorphisms Of Θ-Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-400
-
- Article
-
- You have access
- Export citation
Murnaghan-Nakayama Rules for Characters of Iwahori-Hecke Algebras of the Complex Reflection Groups G(r, p, n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 167-192
-
- Article
-
- You have access
- Export citation
Intertwining Operator and h-Harmonics Associated With Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 193-209
-
- Article
-
- You have access
- Export citation
Imprimitively Generated Lie-Algebraic Hamiltonians and Separation of Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1298-1322
-
- Article
-
- You have access
- Export citation
The Hypercentre and the n-Centre of the Unit Group of an Integral Group Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-411
-
- Article
-
- You have access
- Export citation
Multipliers of Fractional Cauchy Transforms and Smoothness Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 595-604
-
- Article
-
- You have access
- Export citation
Hardy Spaces of Conjugate Systems of Temperatures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 605-619
-
- Article
-
- You have access
- Export citation
Isomorphisms Between Generalized Cartan Type W Lie Algebras in Characteristic 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 210-224
-
- Article
-
- You have access
- Export citation
L’Invariant de Hasse-Witt de la Forme de Killing
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1323-1336
-
- Article
-
- You have access
- Export citation
Asymptotic Transformations of q-Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 412-425
-
- Article
-
- You have access
- Export citation