A detailed comparison between the Landau and the Dougherty collision operators has been performed by means of Eulerian simulations, in the case of relaxation toward equilibrium of a spatially homogeneous field-free plasma in three-dimensional velocity space. Even though the form of the two collisional operators is evidently different, we found that the collisional evolution of the relevant moments of the particle distribution function (temperature and entropy) are similar in the two cases, once an ‘ad hoc’ time rescaling procedure has been performed. The Dougherty operator is a nonlinear differential operator of the Fokker-Planck type and requires a significantly lighter computational effort with respect to the complete Landau integral; this makes self-consistent simulations of plasmas in presence of collisions affordable, even in the multi-dimensional phase space geometry.

The necessity for compact table-top x-ray sources with higher brightness, shorter wavelength and shorter pulse duration has led to the development of complementary sources based on laser-plasma accelerators, in contrast to conventional accelerators. Relativistic interaction of short-pulse lasers with underdense plasmas results in acceleration of electrons and in consequence in the emission of spatially coherent radiation, which is known in the literature as betatron radiation. In this article, we report on our recent results in the rapidly developing field of secondary x-ray radiation generated by high-energy electron pulses. The betatron radiation is characterized with a novel setup allowing to measure the energy, the spatial energy distribution in the far-field of the beam and the source size in a single laser shot. Furthermore, the polarization state is measured for each laser shot. In this way, the emitted betatron x-rays can be used as a non-invasive diagnostic tool to retrieve very subtle information of the electron dynamics within the plasma wave. Parallel to the experimental work, 3D particle-in-cell simulations were performed, proved to be in good agreement with the experimental results.

We describe a laboratory plasma physics experiment at Los Alamos National Laboratory that uses two merging supersonic plasma jets formed and launched by pulsed-power-driven railguns. The jets can be formed using any atomic species or mixture available in a compressed-gas bottle and have the following nominal initial parameters at the railgun nozzle exit: ne ≈ ni ~ 1016 cm−3, Te ≈ Ti ≈ 1.4 eV, Vjet ≈ 30–100 km/s, mean charge $\bar{Z}$ ≈ 1, sonic Mach number Ms ≡ Vjet/Cs > 10, jet diameter = 5 cm, and jet length ≈20 cm. Experiments to date have focused on the study of merging-jet dynamics and the shocks that form as a result of the interaction, in both collisional and collisionless regimes with respect to the inter-jet classical ion mean free path, and with and without an applied magnetic field. However, many other studies are also possible, as discussed in this paper.

The Sun is a giant particle accelerator. During solar flares, magnetic field energy stored in the corona is suddenly released and transferred to local heating of the coronal plasma, mass motions (e.g. jets) and the generation of energetic particles, i.e. electrons, protons and heavy ions. Basically, a flare occurs as a local enhancement of the emission of electromagnetic radiation from the radio up to the ${\it\gamma}$ -ray range on the Sun. That indicates the production of energetic electrons during flares. NASA’s RHESSI mission has the aim to investigate electron acceleration processes by studying the Sun’s X-ray and ${\it\gamma}$ -ray emission with high spatial, temporal and spectral resolution, i.e. by means of imaging spectroscopy. A substantial part of the energy released during a flare is carried by these energetic electrons. Apart from them, solar energetic particles, i.e. protons and heavy ions, and coronal mass ejections play an important role in the energy budget of a flare. Here, we focus on electron acceleration. The way in which $10^{36}$ electrons are accelerated up to energies beyond 30 keV is one of the open questions in solar physics. A flare is considered as the manifestation of magnetic reconnection in the solar corona. Which mechanisms lead to the production of energetic electrons in the magnetic reconnection region is discussed in this paper. Two of them are described in more detail.

In this study, a theory of free-electron laser (FEL) with a Langmuir wave wiggler in the presence of an axial magnetic field has been presented. The small wavelength of the plasma wave (in the sub-mm range) allows obtaining higher frequency than conventional wiggler FELs. Electron trajectories have been obtained by solving the equations of motion for a single electron. In addition, a fourth-order Runge–Kutta method has been used to simulate the electron trajectories. Employing a perturbation analysis, the dispersion relation for an electromagnetic and space-charge waves has been derived by solving the momentum transfer, continuity, and wave equations. Numerical calculations show that the growth rate increases with increasing the e-beam energy and e-beam density, while it decreases with increasing the strength of the axial guide magnetic field.

Using particle-in-cell (PIC) simulations with a Monte Carlo treatment of the Coulomb collision operator, we study the transition in electron dynamics of magnetic reconnection for various levels of collisionality. The weakly collisional cases considered all fall into the so-called Hall or kinetic regime. Nevertheless, collisions may still alter the electron kinetic physics characteristic of collisionless reconnection, where adiabatic trapping energizes the electrons and leads to strong anisotropy of the electron velocity distribution and pressure. This anisotropy can support extended current sheets, associated with secondary island formation and turbulent flux rope interactions in three dimensional systems. The collisional simulations demonstrate how weak collisions may modify or eliminate these electron structures in the kinetic regimes. While the reconnection rate is not sensitive to the collisionality in the range studied, we find that increasing collisionality reduces the level of electron energization near the reconnection site. Finally, the results provide guidance for new laboratory reconnection experiments that will access the weakly collisional regimes.

We derive equations for the mean entropy and the mean internal energy in low-Mach-number temperature stratified turbulence (i.e. for turbulent convection or stably stratified turbulence), and show that turbulent flux of entropy is given by 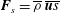$\boldsymbol{F}_{s}=\overline{{\it\rho}}\,\overline{\boldsymbol{u}s}$ , where 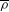$\overline{{\it\rho}}$ is the mean fluid density, $s$ is fluctuation of entropy and overbars denote averaging over an ensemble of turbulent velocity fields, $\boldsymbol{u}$ . We demonstrate that the turbulent flux of entropy is different from the turbulent convective flux, 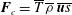$\boldsymbol{F}_{c}=\overline{T}\,\overline{{\it\rho}}\,\overline{\boldsymbol{u}s}$ , of the fluid internal energy, where 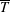$\overline{T}$ is the mean fluid temperature. This turbulent convective flux is well-known in the astrophysical and geophysical literature, and it cannot be used as a turbulent flux in the equation for the mean entropy. This result is exact for low-Mach-number temperature stratified turbulence and is independent of the model used. We also derive equations for the velocity–entropy correlation, 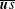$\overline{\boldsymbol{u}s}$ , in the limits of small and large Péclet numbers, using the quasi-linear approach and the spectral ${\it\tau}$ approximation, respectively. This study is important in view of different applications to astrophysical and geophysical temperature stratified turbulence.

Experimental evidence supporting the theory of hot tail runaway electron (RE) generation has been identified in TEXTOR disruptions. With higher temperature, more REs are generated during the thermal quench. Increasing the RE generation by increasing the temperature, an obvious RE plateau is observed even with low toroidal magnetic field (1.7 T). These results explain the previously found electron density threshold for RE generation.

In a tokamak, trapped electrons subject to a strong electric field cannot run away immediately, because their parallel velocity does not increase over a bounce period. However, they do pinch toward the tokamak center. As they pinch toward the center, the trapping cone becomes more narrow, so eventually they can be detrapped and run away. When they run away, trapped electrons will have a very different signature from circulating electrons subject to the Dreicer mechanism. The characteristics of what are called trapped-electron runaways are identified and quantified, including their distinguishable perpendicular velocity spectrum and radial extent.

The behaviour of runaway electrons have been investigated in lower hybrid current drive (LHCD) and electron cyclotron current drive (ECCD) plasmas as well as the LHCD only plasmas in the HL-2A tokamak. The fast electrons generated by lower hybrid waves (LHWs) and electron cyclotron waves (ECWs) can act as a seed population for runaway electrons. In the LHCD only discharges, a large number of runaway electrons are produced after the termination of lower hybrid (LH) power by conversion of fast electrons into runaway electrons due to the fast electron tail which extends above the runaway critical energy. However, in contrast to LHCD only discharges, during the simultaneous application of LHCD and ECCD discharges, runaway electrons cannot be created by the termination of LH power when the ECCD is on duty. The runaway production is observed to be enhanced until the EC power termination. The loop voltage increase due to the termination of EC power gives rise to a decline in the critical runaway energy, which leads to some of the energetic fast electrons converting into runaway electrons via the acceleration from the toroidal electric field. That is, the fast electrons created by waves can be accelerated into the runaway regime due to the Dreicer process.

The plasma immersion ion implantation process is investigated in the presence of q–nonextensive electrons by using a one-dimensional fluid model. The effect of the nonextensivity parameter, q, on the plasma parameters and sheath dynamics during the implantation process is studied. The results show that the implantation dose can be enhanced in the presence of energetic electrons at the tail of the distribution function. Different parameters of plasma such as sheath thickness, ion velocity and ion density show more change at the larger values of the q–parameter. Furthermore, the results of simulation tend to what is predicted by the Maxwellian electron distribution function (q = 1).

For experimental tests of fluctuation theory in ideal plasmas and plasmas seeded with dust, the ideal environment would be that of stable quiescent plasma. In most laboratory plasmas the homogeneous state of the positive column is often unstable, rare exceptions are the so-called brush cathode discharges, proposed in the 60s, where a specially manufactured cathode allows stable operation in the abnormal glow regime and the only fluctuations present are those due the thermal motion of the particles. Such a device, the BAri Brush Electrode (BABE), has recently been built in a novel configuration that combines the advantages of the inverse design with those of the reflex geometry. The region between the two anodes is essentially field-free and extremely stable in wide range of plasma densities and collisionalities. Unprecedented low fluctuation levels of δn/n ⩽ 10−5 in He and δn/n ⩽ 5 × 10−6 in Ar discharges have been achieved.

Accretion disc theory is less developed than stellar evolution theory although a similarly mature phenomenological picture is ultimately desired. While the interplay of theory and numerical simulations has amplified community awareness of the role of magnetic fields in angular momentum transport, there remains a long term challenge to incorporate the insights gained from simulations into improving practical models for comparison with observations. What has been learned from simulations that can lead to improvements beyond SS73 in practical models? Here, we emphasize the need to incorporate the role of non-local transport more precisely. To show where large-scale transport would fit into the theoretical framework and how it is currently missing, we review why the wonderfully practical approach of Shakura & Sunyaev (Astron. Astrophys., vol. 24, 1973, pp. 337–355, SS73) is necessarily a mean field theory, and one which does not include large-scale transport. Observations of coronae and jets, combined with the interpretation of results from shearing box simulations, of the magnetorotational instability (MRI) suggest that a significant fraction of disc transport is indeed non-local. We show that the Maxwell stresses in saturation are dominated by large-scale contributions and that the physics of MRI transport is not fully captured by a viscosity. We also clarify the standard physical interpretation of the MRI as it applies to shearing boxes. Computational limitations have so far focused most attention toward local simulations, but the next generation of global simulations should help to inform improved mean field theories. Mean field accretion theory and mean field dynamo theory should in fact be unified into a single theory that predicts the time evolution of spectra and luminosity from separate disc, corona and outflow contributions. Finally, we note that any mean field theory, including that of SS73, has a finite predictive precision that needs to be quantified when comparing the predictions to observations.

Space plasma physics, pushed by the impressive recent technological developments, is undergoing a period of intense progress. This progress is achieved first at the level of observations, including both remote and in situ measurements, but also on the theoretical side, mainly by means of large scale numerical simulations made possible by the dramatic increase of computational resources. In particular, three-dimensional mainly hybrid but also fully kinetic simulations are today feasible, and large intervals in spatial and time scales can at last be accessed by fluid simulations. Addressing fundamental problems such as, e.g. magnetic reconnection, nonlinear dynamics or turbulence development in the kinetic range, are no longer just a heart's desire today.

Stability of the plane tangential discontinuity (TD) interface in a multi-component dusty plasma (ions, electrons, neutral particles and charged dust) is considered in hydrodynamical approximation. The criterion of stability does not depend on the presence of dust only on one side of the discontinuity but is changed if the dust penetrates through the discontinuity. Therefore, if the instability criterion is marginal, even weak penetration of the dust through the interface may induce Kelvin–Helmholtz instability. This conclusion also refers to cylindrical TD in the presence of dust, so that generation of helical waves in astrophysical jets, type I comet tails, etc. due to the shear driven Kelvin–Helmholtz instability may be hampered in dusty objects of such a geometry.

In a quasineutral plasma, electrons undergo collective oscillations, known as plasma oscillations, when perturbed locally. The oscillations propagate due to finite temperature effects. However, the wave can lose the phase coherence between constituting oscillators in an inhomogeneous plasma (phase mixing) because of the dependence of plasma oscillation frequency on plasma density. The longitudinal electric field associated with the wave may be used to accelerate electrons to high energies by exciting large amplitude wave. However when the maximum amplitude of the wave is reached that plasma can sustain, the wave breaks. The phenomena of wave breaking and phase mixing have applications in plasma heating and particle acceleration. For detailed experimental investigation of these phenomena a new device, inverse mirror plasma experimental device (IMPED), has been designed and fabricated. The detailed considerations taken before designing the device, so that different aspects of these phenomena can be studied in a controlled manner, are described. Specifications of different components of the IMPED machine and their flexibility aspects in upgrading, if necessary, are discussed. Initial results meeting the prerequisite condition of the plasma for such study, such as a quiescent, collisionless and uniform plasma, are presented. The machine produces δnnoise/n ⩽ 1%, Luniform ~ 120 cm at argon filling pressure of ~10−4 mbar and axial magnetic field of B = 1090 G.

The long-term evolution of large-amplitude Alfvén waves propagating in the solar wind is investigated by performing two-dimensional MHD simulations within the expanding box model. The linear and nonlinear phases of the parametric decay instability are studied for both circularly polarized waves in parallel propagation and for arc-polarized waves in oblique propagation. The non-monochromatic case is also considered. In the oblique case, the direct excitation of daughter modes transverse to the local background field is found for the first time in an expanding environment, and this transverse cascade seems to be favored for monochromatic mother waves. The expansion effect reduces the instability growth rate, and it can even suppress its onset for the lowest frequency modes considered here, possibly explaining the persistence of these outgoing waves in the solar wind.

The effects of an imposed, axial magnetic field $B_{z0}$ on hydrodynamics and energetic electrons in inertial confinement fusion indirect-drive hohlraums are studied. We present simulations from the radiation-hydrodynamics code HYDRA of a low-adiabat ignition design for the National Ignition Facility, with and without $B_{z0}=70~\text{T}$ . The field’s main hydrodynamic effect is to significantly reduce electron thermal conduction perpendicular to the field. This results in hotter and less dense plasma on the equator between the capsule and hohlraum wall. The inner laser beams experience less inverse bremsstrahlung absorption before reaching the wall. The X-ray drive is thus stronger from the equator with the imposed field. We study superthermal, or ‘hot’, electron dynamics with the particle-in-cell code ZUMA, using plasma conditions from HYDRA. During the early-time laser picket, hot electrons based on two-plasmon decay in the laser entrance hole (Regan et al., Phys. Plasmas, vol. 17(2), 2010, 020703) are guided to the capsule by a 70 T field. Twelve times more energy deposits in the deuterium–tritium fuel. For plasma conditions early in peak laser power, we present mono-energetic test-case studies with ZUMA  as well as sources based on inner-beam stimulated Raman scattering. The effect of the field on deuterium–tritium deposition depends strongly on the source location, namely whether hot electrons are generated on field lines that connect to the capsule.

The particle-in-cell (PIC) algorithm is the most popular method for the discretisation of the general 6D Vlasov–Maxwell problem and it is widely used also for the simulation of the 5D gyrokinetic equations. The method consists of coupling a particle-based algorithm for the Vlasov equation with a grid-based method for the computation of the self-consistent electromagnetic fields. In this review we derive a Monte Carlo PIC finite-element model starting from a gyrokinetic discrete Lagrangian. The variations of the Lagrangian are used to obtain the time-continuous equations of motion for the particles and the finite-element approximation of the field equations. The Noether theorem for the semi-discretised system implies a certain number of conservation properties for the final set of equations. Moreover, the PIC method can be interpreted as a probabilistic Monte Carlo like method, consisting of calculating integrals of the continuous distribution function using a finite set of discrete markers. The nonlinear interactions along with numerical errors introduce random effects after some time. Therefore, the same tools for error analysis and error reduction used in Monte Carlo numerical methods can be applied to PIC simulations.

We examine the impact of several factors on electron acceleration by a laser pulse and the resulting electron energy gain. Specifically, we consider the role played by: (1) static longitudinal electric field, (2) static transverse electric field, (3) electron injection into the laser pulse, and (4) static longitudinal magnetic field. It is shown that all of these factors lead, under certain conditions, to a considerable electron energy gain from the laser pulse. In contrast with other mechanisms such as wakefield acceleration, the static electric fields in this case do not directly transfer substantial energy to the electron. Instead, they reduce the longitudinal dephasing between the electron and the laser beam, which then allows the electron to gain extra energy from the beam. The mechanisms discussed here are relevant to experiments with under-dense gas jets, as well as to experiments with solid-density targets involving an extended pre-plasma.