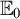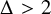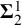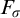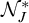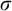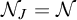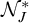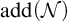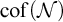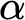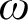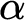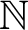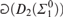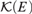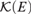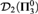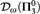26 results
BOREL LINE GRAPHS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEBESGUE MEASURE ZERO MODULO IDEALS ON THE NATURAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 December 2023, pp. 1-31
-
- Article
- Export citation
DENSITY-LIKE AND GENERALIZED DENSITY IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 228-251
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECURRENCE AND THE EXISTENCE OF INVARIANT MEASURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 60-76
- Print publication:
- March 2021
-
- Article
- Export citation
Minimal definable graphs of definable chromatic number at least three
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 January 2021, e7
-
- Article
-
- You have access
- Open access
- Export citation
SHORTENING CLOPEN GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1541-1554
- Print publication:
- December 2021
-
- Article
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
BASES FOR FUNCTIONS BEYOND THE FIRST BAIRE CLASS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1289-1303
- Print publication:
- September 2020
-
- Article
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
ON THE EXISTENCE OF LARGE ANTICHAINS FOR DEFINABLE QUASI-ORDERS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 103-108
- Print publication:
- March 2020
-
- Article
- Export citation
THE GAME OPERATOR ACTING ON WADGE CLASSES OF BOREL SETS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1224-1239
- Print publication:
- September 2019
-
- Article
- Export citation
On the existence of cocycle-invariant Borel probability measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 12 April 2019, pp. 3150-3168
- Print publication:
- November 2020
-
- Article
- Export citation
Gδ Sets IN σ-IDEALS GENERATED BY COMPACT SETS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 March 2019, pp. 781-797
- Print publication:
- June 2019
-
- Article
- Export citation
MEASURABLE PERFECT MATCHINGS FOR ACYCLIC LOCALLY COUNTABLE BOREL GRAPHS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 258-271
- Print publication:
- March 2017
-
- Article
- Export citation
NORMAL NUMBERS AND COMPLETENESS RESULTS FOR DIFFERENCE SETS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 247-257
- Print publication:
- March 2017
-
- Article
- Export citation
HANDMADE DENSITY SETS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 208-223
- Print publication:
- March 2017
-
- Article
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Krein-Smulian-Type Theorems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 441-444
-
- Article
- Export citation
NOTE ABOUT LINDELÖF Σ-SPACES υX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 28 September 2011, pp. 114-120
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation