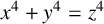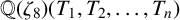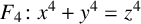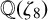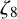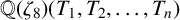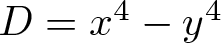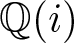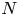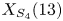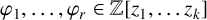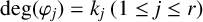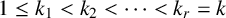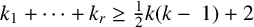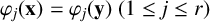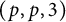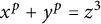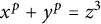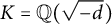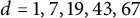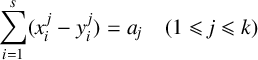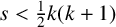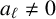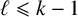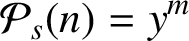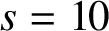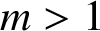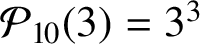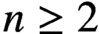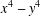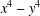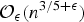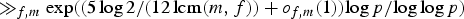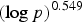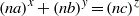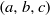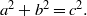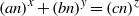42 results
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINTS ON
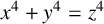 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 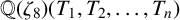 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
On the difference of two fourth powers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 142-150
-
- Article
-
- You have access
- HTML
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 29-39
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ternary Diophantine equations of signature
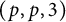 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1293-1313
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Ineffective Results for Diophantine Equations over Finitely Generated Domains
-
- Book:
- Effective Results and Methods for Diophantine Equations over Finitely Generated Domains
- Published online:
- 31 August 2022
- Print publication:
- 28 April 2022, pp 1-17
-
- Chapter
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON REPUNIT CULLEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 264-268
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON THE K-RATIONAL DISTANCE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 01 December 2020, pp. 40-44
- Print publication:
- August 2021
-
- Article
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation
INTEGERS REPRESENTED BY
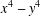 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
- Print publication:
- February 2021
-
- Article
- Export citation
The number of solutions of the Erdős-Straus Equation and sums of k unit fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1401-1427
- Print publication:
- June 2020
-
- Article
- Export citation
Construction of ray-class fields by smaller generators and their applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 781-812
- Print publication:
- August 2017
-
- Article
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES – CORRIGENDUM
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 01 August 2014, p. 751
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
RATIONAL POINTS ON INTERSECTIONS OF CUBIC AND QUADRIC HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 05 June 2014, pp. 703-749
- Print publication:
- October 2015
-
- Article
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
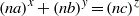 $\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
$\mathop{(na)}\nolimits ^{x} + \mathop{(nb)}\nolimits ^{y} = \mathop{(nc)}\nolimits ^{z} $
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 August 2013, pp. 316-321
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
A DIOPHANTINE PROBLEM CONCERNING POLYGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 345-350
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
APPROXIMATION OF AN ALGEBRAIC NUMBER BY PRODUCTS OF RATIONAL NUMBERS AND UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 121-131
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation