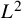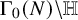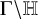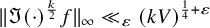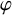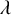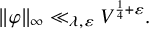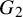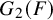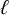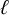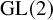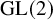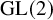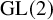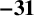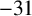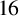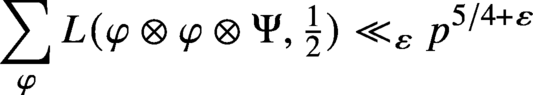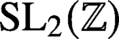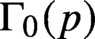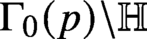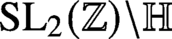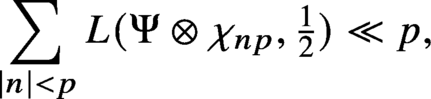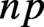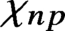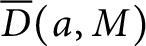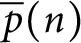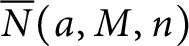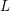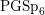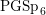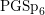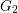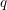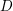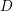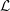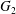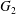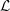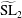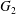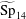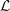51 results
On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2115-2202
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Local Langlands Conjecture for
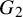 $G_2$
$G_2$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Kudla–Millson form via the Mathai–Quillen formalism
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 1638-1663
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hodge classes and the Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 September 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exotic Monoidal Structures and Abstractly Automorphic Representations for
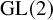 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shintani lifts of nearly holomorphic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 1446-1492
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN APPLICATION OF BINARY QUADRATIC FORMS OF DISCRIMINANT
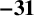 $\boldsymbol {-31}$
TO MODULAR FORMS
$\boldsymbol {-31}$
TO MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 269-272
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
Dyson’s rank, overpartitions, and universal mock theta functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 687-696
- Print publication:
- September 2021
-
- Article
- Export citation
Local intertwining relation for metaplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1560-1594
- Print publication:
- August 2020
-
- Article
- Export citation
ANALYTIC PROPERTIES OF EISENSTEIN SERIES AND STANDARD
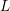 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 168-203
- Print publication:
- December 2021
-
- Article
- Export citation
An exceptional Siegel–Weil formula and poles of the Spin L-function of
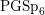 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
PERIOD IDENTITIES OF CM FORMS ON QUATERNION ALGEBRAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 May 2020, e25
-
- Article
-
- You have access
- Open access
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation
On some incomplete theta integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1711-1746
- Print publication:
- September 2019
-
- Article
- Export citation
Poles of the Standard
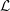 ${\mathcal{L}}$-function of
${\mathcal{L}}$-function of 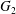 $G_{2}$ and the Rallis–Schiffmann Lift
$G_{2}$ and the Rallis–Schiffmann Lift
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1127-1161
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation