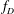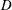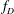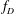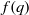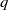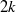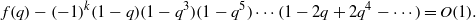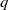31 results
L-series for Vector-Valued Weakly Holomorphic Modular Forms and Converse Theorems
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 January 2025, pp. 1-26
-
- Article
- Export citation
Eichler–Selberg relations for singular moduli
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR RANKS OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 280-290
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Shintani lifts of nearly holomorphic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 1446-1492
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL CUSP FORMS OF DEGREE 2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1819-1869
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation
RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 157-175
- Print publication:
- October 2020
-
- Article
- Export citation
Newforms of Half-integral Weight: The Minus Space Counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 31 October 2019, pp. 326-372
- Print publication:
- April 2020
-
- Article
- Export citation
A CONVERSE THEOREM FOR BORCHERDS PRODUCTS ON
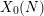 $X_{0}(N)$
$X_{0}(N)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 01 March 2019, pp. 237-256
- Print publication:
- December 2020
-
- Article
- Export citation
A CERTAIN DIRICHLET SERIES OF RANKIN–SELBERG TYPE ASSOCIATED WITH THE IKEDA LIFT OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 17 June 2019, pp. 897-928
- Print publication:
- 2019
-
- Article
- Export citation
ON THE STANDARD TWIST OF THE
 $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
$L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 150-180
- Print publication:
- December 2020
-
- Article
- Export citation
RANKIN–SELBERG CONVOLUTIONS OF NONCUSPIDAL HALF-INTEGRAL WEIGHT MAASS FORMS IN THE PLUS SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 21 May 2018, pp. 127-165
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
PARTIAL INDEFINITE THETA IDENTITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 255-289
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON SIGN CHANGES FOR ALMOST PRIME COEFFICIENTS OF HALF-INTEGRAL WEIGHT MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 801-810
- Print publication:
- 2016
-
- Article
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
- Print publication:
- 2016
-
- Article
- Export citation
Values of Twisted Tensor L-functions of Automorphic Forms Over Imaginary Quadratic Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1078-1109
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
Modular forms of half-integral weights on SL(2, ℤ)
-
- Journal:
- Nagoya Mathematical Journal / Volume 215 / September 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-66
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
On a completed generating function of locally harmonic Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 26 March 2014, pp. 749-762
- Print publication:
- May 2014
-
- Article
- Export citation
MOCK THETA FUNCTIONS AND QUANTUM MODULAR FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 1 / 2013
- Published online by Cambridge University Press:
- 19 September 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation

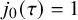
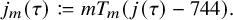
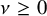
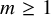
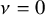
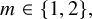
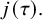
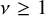
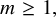
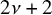
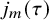
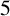
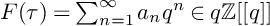
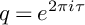
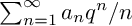
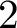
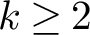
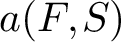
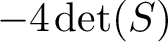
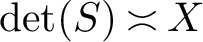
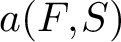
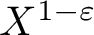
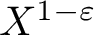
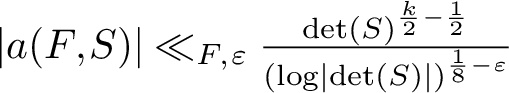
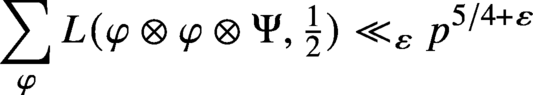
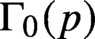
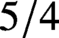
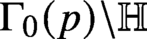
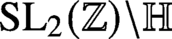
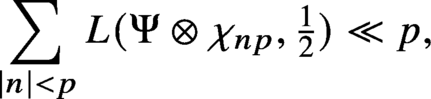
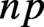
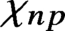
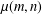
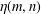


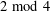
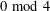
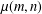
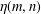
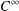
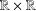
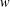
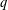

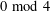
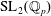
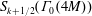
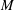
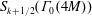
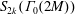
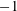
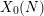
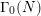
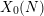
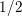
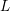
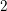
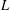
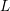
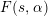
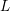
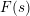
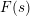
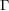
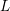
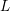
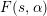

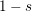
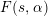
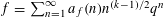
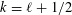
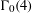
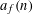
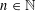

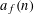


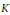
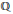
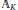

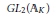
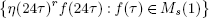
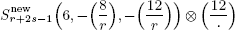
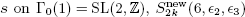 is the space of newforms of weight 2
is the space of newforms of weight 2