14 results
A revisit to “On BMO and Carleson measures on Riemannian manifolds”
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 18 July 2023, pp. 1281-1307
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Maximal operators on BMO and slices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 94-107
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Muckenhoupt Class Weight Decomposition and BMO Distance to Bounded Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 25 March 2019, pp. 1017-1031
-
- Article
- Export citation
VMO Space Associated with Parabolic Sections and its Application
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 3 / 01 September 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-518
- Print publication:
- 01 September 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
EXPLICIT INTERPOLATION BOUNDS BETWEEN HARDY SPACE AND
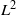 ${L}^{2} $
${L}^{2} $
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 158-168
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
SHARP ESTIMATES FOR FUNCTIONS OF BOUNDED LOWER OSCILLATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2012, pp. 68-81
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ENDPOINT ESTIMATES FOR COMMUTATORS OF RIESZ TRANSFORMS ASSOCIATED WITH SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 367-389
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
BMO Functions and Carleson Measures with Values in Uniformly Convex Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 827-844
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
THE RATE OF INCREASE OF MEAN VALUES OF FUNCTIONS IN HARDY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 199-204
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Boundedness of vector-valued martingale transforms on extreme points and applciations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-222
- Print publication:
- April 2004
-
- Article
-
- You have access
- Export citation
Commutators and Analytic Dependence of Fourier-Bessel Series on (0, ∞)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 2 / 01 June 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 198-208
- Print publication:
- 01 June 1999
-
- Article
-
- You have access
- Export citation
Rearrangements of the Haar system that preserve BMO
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 75 / Issue 3 / November 1997
- Published online by Cambridge University Press:
- 01 November 1997, pp. 600-618
- Print publication:
- November 1997
-
- Article
- Export citation
On an equivalent class of norms for BMO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-295
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation

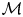
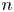
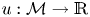
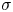
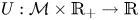
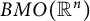
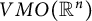
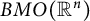
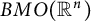
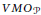
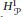

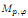 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global 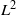
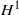
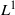
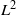
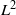
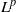
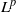
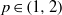
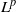
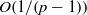
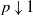
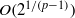
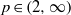
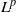
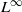
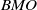
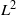
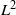
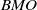
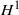
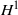
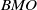

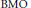
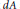
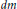
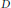
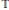
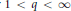
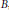

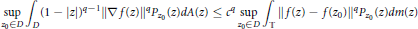
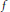

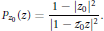
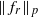 as
as 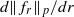 grows at most like
grows at most like 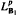 into
into 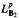 for some
for some 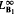 into
into 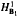 into
into 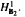 . Applications to
. Applications to 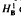 defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.
defined in the case of a general filtration has nice dense sets and nice atomic decompositions if and only if Β has the Radon-Nikodým property.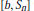

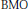
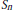
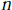
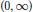
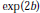
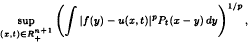
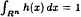 and
and 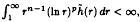 , where
, where 