118 results
Voice processing ability predicts second-language phoneme learning in early bilingual adults
-
- Journal:
- Bilingualism: Language and Cognition , First View
- Published online by Cambridge University Press:
- 17 January 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Note on Structural Models for the Circumplex
-
- Journal:
- Psychometrika / Volume 51 / Issue 1 / March 1986
- Published online by Cambridge University Press:
- 01 January 2025, pp. 143-147
-
- Article
- Export citation
Heterogeneous Factor Analysis Models: A Bayesian Approach
-
- Journal:
- Psychometrika / Volume 67 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 01 January 2025, pp. 49-77
-
- Article
- Export citation
Rotational Equivalence of Factor Loading Matrices with Specified Values
-
- Journal:
- Psychometrika / Volume 43 / Issue 3 / September 1978
- Published online by Cambridge University Press:
- 01 January 2025, pp. 421-426
-
- Article
- Export citation
Estimation of Covariance Structure Models with Parameters Subject to Functional Restraints
-
- Journal:
- Psychometrika / Volume 45 / Issue 3 / September 1980
- Published online by Cambridge University Press:
- 01 January 2025, pp. 309-324
-
- Article
- Export citation
Multilevel Heterogeneous Factor Analysis and Application to Ecological Momentary Assessment
-
- Journal:
- Psychometrika / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 01 January 2025, pp. 75-100
-
- Article
- Export citation
Implications of Indeterminate Factor-Error Covariances for Factor Construction, Prediction, and Determinacy
-
- Journal:
- Psychometrika / Volume 71 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 January 2025, pp. 503-519
-
- Article
- Export citation
Nonparametric Estimation of Standard Errors in Covariance Analysis Using the Infinitesimal Jackknife
-
- Journal:
- Psychometrika / Volume 73 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 January 2025, pp. 579-594
-
- Article
- Export citation
Improper Solutions in the Analysis of Covariance Structures: Their Interpretability and a Comparison of Alternate Respecifications
-
- Journal:
- Psychometrika / Volume 52 / Issue 1 / March 1987
- Published online by Cambridge University Press:
- 01 January 2025, pp. 99-111
-
- Article
- Export citation
A Note on Some Equations of Confirmatory Factor Analysis
-
- Journal:
- Psychometrika / Volume 36 / Issue 1 / March 1971
- Published online by Cambridge University Press:
- 01 January 2025, pp. 63-70
-
- Article
- Export citation
Identification with Deficient Rank Loading Matrices in Confirmatory Factor Analysis: Multitrait-Multimethod Models
-
- Journal:
- Psychometrika / Volume 59 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 January 2025, pp. 121-134
-
- Article
- Export citation
Necessary Conditions for Mean Square Convergence of the Best Linear Factor Predictor
-
- Journal:
- Psychometrika / Volume 71 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 01 January 2025, pp. 593-599
-
- Article
- Export citation
Some Results on Mean Square Error for Factor Score Prediction
-
- Journal:
- Psychometrika / Volume 71 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 01 January 2025, pp. 395-409
-
- Article
- Export citation
A Note on the Identification of Restricted Factor Loading Matrices
-
- Journal:
- Psychometrika / Volume 51 / Issue 4 / December 1986
- Published online by Cambridge University Press:
- 01 January 2025, pp. 607-611
-
- Article
- Export citation
Convergence of Estimates of Unique Variances in Factor Analysis, Based on the Inverse Sample Covariance Matrix
-
- Journal:
- Psychometrika / Volume 71 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 01 January 2025, pp. 193-199
-
- Article
- Export citation
An Alternative to the Methodology for Analysis of Covariance
-
- Journal:
- Psychometrika / Volume 43 / Issue 3 / September 1978
- Published online by Cambridge University Press:
- 01 January 2025, pp. 381-396
-
- Article
- Export citation
Determinants of Standard Errors of MLEs in Confirmatory Factor Analysis
-
- Journal:
- Psychometrika / Volume 75 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 01 January 2025, pp. 633-648
-
- Article
- Export citation
On the Construction of all Factors of the Model for Factor Analysis
-
- Journal:
- Psychometrika / Volume 67 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 01 January 2025, pp. 161-172
-
- Article
- Export citation
A General Theorem and Proof for the Identification of Composed CFA Models
-
- Journal:
- Psychometrika / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1334-1353
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Bayesian Estimation of Factor Score in Confirmatory Factor Model with Polytomous, Censored or Truncated Data
-
- Journal:
- Psychometrika / Volume 62 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 January 2025, pp. 29-50
-
- Article
- Export citation

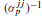 tends to the corresponding unique variance ψ
tends to the corresponding unique variance ψ
