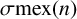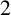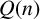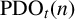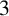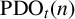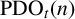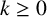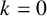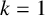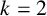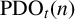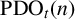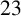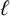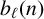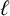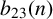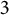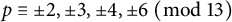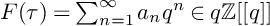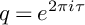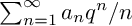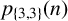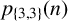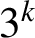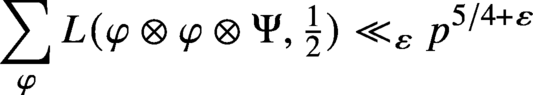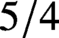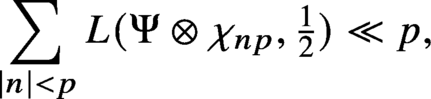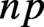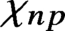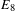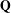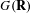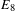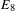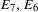Refine search
Actions for selected content:
69 results
FURTHER ARITHMETIC PROPERTIES OF OVERCUBIC PARTITION TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 260-273
- Print publication:
- October 2025
-
- Article
- Export citation
1 - Introduction
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 1-6
-
- Chapter
- Export citation

Modular Forms and String Theory
-
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024
Kato’s main conjecture for potentially ordinary primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 338-358
- Print publication:
- May 2024
-
- Article
- Export citation
GENERALISED AUTOMORPHIC SHEAVES AND THE PROPORTIONALITY PRINCIPLE OF HIRZEBRUCH-MUMFORD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 1567-1605
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE FOR A REFINEMENT OF THE SUM OF MINIMAL EXCLUDANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 July 2023, pp. 276-287
- Print publication:
- April 2024
-
- Article
- Export citation
A CONJECTURE OF MERCA ON CONGRUENCES MODULO POWERS OF 2 FOR PARTITIONS INTO DISTINCT PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 26-36
- Print publication:
- February 2024
-
- Article
- Export citation
DIVISIBILITY OF THE PARTITION FUNCTION
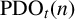 $\text {PDO}_t(n)$ BY POWERS OF
$\text {PDO}_t(n)$ BY POWERS OF 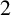 $2$ AND
$2$ AND 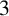 $3$
$3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 March 2023, pp. 14-25
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
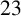 $23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
$23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 254-263
- Print publication:
- October 2023
-
- Article
- Export citation
Modular forms and some cases of the Inverse Galois Problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 568-586
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix D - Modular Forms and Special Functions
-
- Book:
- A Short Introduction to String Theory
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 244-246
-
- Chapter
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation
Eisenstein metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 778-803
- Print publication:
- June 2023
-
- Article
- Export citation
ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 385-391
- Print publication:
- June 2022
-
- Article
- Export citation
9 - Further Work and the Epilogue
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 451-464
-
- Chapter
- Export citation
DIVISIBILITY OF CERTAIN SINGULAR OVERPARTITIONS BY POWERS OF
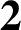 $\textbf{2}$ AND
$\textbf{2}$ AND 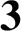 $\textbf{3}$
$\textbf{3}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 238-248
- Print publication:
- October 2021
-
- Article
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation
THE MINIMAL MODULAR FORM ON QUATERNIONIC
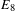 $E_{8}$
$E_{8}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 603-636
- Print publication:
- March 2022
-
- Article
- Export citation
The Modularity of Special Cycles on Orthogonal Shimura Varieties over Totally Real Fields under the Beilinson–Bloch Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 39-53
- Print publication:
- March 2021
-
- Article
- Export citation