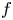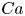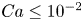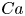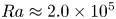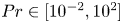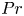174 results
Ribbing patterns in inertial rotary drag-out
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 21 March 2025, A84
-
- Article
- Export citation
Impact of prey-taxis on a harvested intraguild predation predator–prey model
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Turing heritage for plant biology: all spots and stripes?
-
- Journal:
- Quantitative Plant Biology / Volume 6 / 2025
- Published online by Cambridge University Press:
- 13 January 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling analysis for the frequency of Ostwaldian and Newtonian bead-on-fibre flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1002 / 10 January 2025
- Published online by Cambridge University Press:
- 26 December 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
15 - Externally Controllable Molecular Communication
-
- Book:
- Molecular Communication
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 270-292
-
- Chapter
- Export citation
Natural convection in a vertical channel. Part 1. Wavenumber interaction and Eckhaus instability in a narrow domain
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Natural convection in a vertical channel. Part 2. Oblique solutions and global bifurcations in a spanwise-extended domain
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear evolution of vortical disturbances entrained in the entrance region of a circular pipe
-
- Journal:
- Journal of Fluid Mechanics / Volume 998 / 10 November 2024
- Published online by Cambridge University Press:
- 29 October 2024, A19
-
- Article
-
- You have access
- HTML
- Export citation
Gravity-driven flow of liquid bridges between vertical fibres
-
- Journal:
- Journal of Fluid Mechanics / Volume 997 / 25 October 2024
- Published online by Cambridge University Press:
- 23 October 2024, A74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instabilities and particle-induced patterns in co-rotating suspension Taylor–Couette flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 995 / 25 September 2024
- Published online by Cambridge University Press:
- 19 September 2024, R4
-
- Article
-
- You have access
- HTML
- Export citation
A crystallographic approach to symmetry-breaking in fluid layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 989 / 25 June 2024
- Published online by Cambridge University Press:
- 29 July 2024, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuation covariance-based study of roll-streak dynamics in Poiseuille flow turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 988 / 10 June 2024
- Published online by Cambridge University Press:
- 31 May 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Snap-induced flow in a closed channel
-
- Journal:
- Journal of Fluid Mechanics / Volume 986 / 10 May 2024
- Published online by Cambridge University Press:
- 02 May 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emergence of a hexagonal pattern in shear-thickening suspensions under orbital oscillations
-
- Journal:
- Journal of Fluid Mechanics / Volume 984 / 10 April 2024
- Published online by Cambridge University Press:
- 12 April 2024, A69
-
- Article
-
- You have access
- HTML
- Export citation
From a vortex gas to a vortex crystal in instability-driven two-dimensional turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 984 / 10 April 2024
- Published online by Cambridge University Press:
- 08 April 2024, A41
-
- Article
-
- You have access
- HTML
- Export citation
Bifurcations and pattern formation in a host–parasitoid model with nonlocal effect
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1-40
-
- Article
-
- You have access
- HTML
- Export citation
Supergranule aggregation: a Prandtl number-independent feature of constant heat flux-driven convection flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 980 / 10 February 2024
- Published online by Cambridge University Press:
- 06 February 2024, A46
-
- Article
-
- You have access
- HTML
- Export citation
Particle-size segregation patterns in a partially filled triangular rotating drum
-
- Journal:
- Journal of Fluid Mechanics / Volume 979 / 25 January 2024
- Published online by Cambridge University Press:
- 18 January 2024, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern evolution and modal decomposition of Faraday waves in a brimful cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 974 / 10 November 2023
- Published online by Cambridge University Press:
- 10 November 2023, A56
-
- Article
- Export citation
Thermo-electric convection in a cylindrical annulus during a sounding rocket flight
-
- Journal:
- Journal of Fluid Mechanics / Volume 972 / 10 October 2023
- Published online by Cambridge University Press:
- 03 October 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation