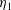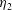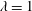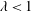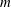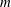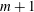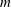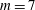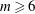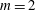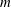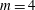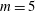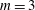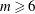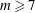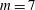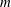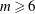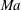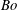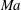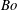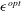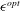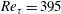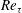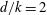Contents
JFM Rapids
Turbulent drag reduction by compliant lubricating layer
-
- Published online by Cambridge University Press:
- 24 January 2019, R1
-
- Article
- Export citation
Scale-invariant singularity of the surface quasigeostrophic patch
-
- Published online by Cambridge University Press:
- 28 January 2019, R2
-
- Article
- Export citation
JFM Papers
The singularity method in unsteady Stokes flow: hydrodynamic force and torque around a sphere in time-dependent flows
-
- Published online by Cambridge University Press:
- 22 January 2019, pp. 1-31
-
- Article
- Export citation
Three-dimensional quasi-geostrophic vortex equilibria with
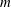 $m$-fold symmetry
$m$-fold symmetry
-
- Published online by Cambridge University Press:
- 22 January 2019, pp. 32-59
-
- Article
- Export citation
The stability and nonlinear evolution of quasi-geostrophic toroidal vortices
-
- Published online by Cambridge University Press:
- 22 January 2019, pp. 60-78
-
- Article
- Export citation
Large-eddy simulation of temporally developing double helical vortices
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 79-113
-
- Article
- Export citation
Weakly nonlinear transient waves on a shear current: ring waves and skewed Langmuir rolls
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 114-149
-
- Article
- Export citation
Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 1. ‘Long-wave’ regimes
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 150-184
-
- Article
- Export citation
Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 2. Mid-wave regimes
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 185-214
-
- Article
- Export citation
The interaction between a spatially oscillating jet emitted by a fluidic oscillator and a cross-flow
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 215-241
-
- Article
- Export citation
An analytical model for asymmetric Mach reflection configuration in steady flows
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 242-268
-
- Article
- Export citation
Filtered lifting line theory and application to the actuator line model
-
- Published online by Cambridge University Press:
- 23 January 2019, pp. 269-292
-
- Article
- Export citation
The influence of the chemical composition representation according to the number of species during mixing in high-pressure turbulent flows
-
- Published online by Cambridge University Press:
- 24 January 2019, pp. 293-340
-
- Article
- Export citation
Direct numerical simulation of backward-facing step flow at
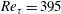 $Re_{\unicode[STIX]{x1D70F}}=395$ and expansion ratio 2
$Re_{\unicode[STIX]{x1D70F}}=395$ and expansion ratio 2
-
- Published online by Cambridge University Press:
- 24 January 2019, pp. 341-363
-
- Article
- Export citation
Equilibrium configurations of drops or bubbles in an eccentric annulus
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 364-385
-
- Article
- Export citation
Experiments on a jet in a crossflow in the low-velocity-ratio regime
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 386-406
-
- Article
- Export citation
Modelling smooth- and transitionally rough-wall turbulent channel flow by leveraging inner–outer interactions and principal component analysis
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 407-453
-
- Article
- Export citation
The amplification of large-scale motion in a supersonic concave turbulent boundary layer and its impact on the mean and statistical properties
-
- Published online by Cambridge University Press:
- 29 January 2019, pp. 454-493
-
- Article
- Export citation
Drag forces on a bed particle in open-channel flow: effects of pressure spatial fluctuations and very-large-scale motions
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 494-512
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracking vortex surfaces frozen in the virtual velocity in non-ideal flows
-
- Published online by Cambridge University Press:
- 25 January 2019, pp. 513-544
-
- Article
- Export citation